階層ベイズで東京23区のお部屋の家賃相場を推定する
はじめに
この記事は確率的プログラミング言語 Advent Calendar 2023の19日目の記事です。松浦先生、主催いただきありがとうございます。今回は参加できてうれしく思います。6日遅れての投稿で恐縮ですがどうぞよろしくお願いいたします。
SUUMOからスクレイピングした東京23区の20万件程度の賃貸物件のデータを用いて、最寄り駅で階層化した家賃の階層モデルをStanで実装して家賃相場を推定してみました。
スクレイピングはPython + requests + BeautifulSoup4、それ以降の分析パートはR + Stan (rstan) で実装しました。Stanの可視化にはbayesplotやtidybayesを使っています。
データ取得や前処理、可視化の部分がだいぶ長くなってしまいましたので、モデルの推定や結果については「モデリング」の章からご覧ください。
追記: 続きの記事を書きました。部屋の階数は家賃にどれだけ影響を与えるのか? - suzuna's memo
モデリングの動機
部屋を探すとき、都心に住みたいけど高いなあ、じゃあこの路線沿いで都心から離れるほどどのくらい家賃相場が変わるの?とか、新築は高いなあ、築年数を広げるとどのくらい家賃が下がるの?とか、一度は考えたことはないでしょうか?
何々駅の家賃相場は1LDKでいくらという情報はググれば見つけられます。大まかな家賃相場を理解するために有用な情報なのですが、築年数や駅からの距離によって当然相場は変わってきます。築浅がいい、逆に古くてもいいから安くしたいとか、絶対駅近がいい、駅から離れていてもいいとか、人によって好みがあります。
また、築浅物件が多い街、そうではない街という違いもあります。単純に平均すると、築年数の影響で後者の街の家賃相場が下がってしまうので、築年数の影響を除いた相場も知りたいですね1。
それに、例えば1LDKと言っても面積は物件によって様々です。40m2の1LDKと50m2の1LDKでは、他の条件が同じなら当然後者の方が高いです。なので、例えば最寄り駅がここで面積はいくつで築年数が何年で徒歩何分の物件はいくらかという情報が知りたくなるところです。
直感的には、同じ最寄り駅の物件に限定すると、家賃は面積の単調増加、築年数と最寄り駅からの徒歩分数の単調減少な関数であり、地価の違いからこの回帰直線は物件の最寄り駅によって上下動するように思われます。階層ベイズにぴったりのテーマのように思われます。
わたしが知りたいのは以下の内容です。
- 築年数が1年増えると家賃がどの程度下がるのか
- 駅からの徒歩分数が1分増えると家賃がどの程度下がるのか
- 築年数、徒歩分数、面積を固定したとき、最寄り駅によってどの程度家賃相場が変わるのか
- 面積を変えるとどの程度家賃相場が変わるのか
これが分かれば、任意の築年数、徒歩分数、面積、最寄り駅での家賃相場を推定することができます。
というわけで、自分が知りたくなったのでStanで実装してみました。
環境
- R 4.3.1
- rstan 2.32.3
- bayesplot 1.10.0
- tidybayes 3.0.6
- furrr 0.3.1
- MLmetrics 1.1.1
問題設定
目的変数と説明変数
対象は東京23区の賃貸物件です。
目的変数を家賃+管理費とするモデルを組むことにします。要するに毎月発生する費用です。敷金や礼金は考慮しないこととします2。以下断りがない限り「家賃」は「家賃+管理費」を指します。
使える説明変数は、SUUMOでスクレイピングした物件リストのページに存在する以下の項目です。今回のモデリングではこの中でも使っていない変数もあります。
- 住所(「東京都千代田区千代田1」の粒度まで)
- 専有面積
- 築年数
- 最寄り駅の路線、駅名、駅からの徒歩の分数
- 最大3つの最寄り駅が記載されている
- 間取り(1LDKとか)
- 建物の高さ(地上x階地下y階建てのxとy)
- 部屋の階数
敷金や礼金も取得できますが、説明変数には使用しません。敷金や礼金はたいてい家賃の0~2ヶ月分なので、これを説明変数に入れると家賃+管理費はある程度予測できてしまうからです。ある意味Leakageですね。
SUUMOの物件ごとのページには以下の項目も記載されていますが、このページもスクレイピングしようとするとスクレイピングにかかる時間が膨れ上がるため、今回はスクレイピングせず使用しませんでした。
- 部屋の特徴・設備
- バストイレ別や浴室乾燥機があるかどうか、角部屋かどうかなど
- 部屋の方角
- 建物の構造(鉄筋や鉄骨など)
- 近所のコンビニやスーパーマーケットなどの店名と物件からそこまでの距離
- 部屋の画像
- 敷金・礼金以外のその他の初期費用
分析の流れ
以下の流れで進めていきます。
- データの取得(SUUMOのスクレイピング)
- 前処理
- 可視化(探索的データ分析)
- 可視化の結果をもとにモデルを定式化
- MCMCでのモデルのパラメータ推定
- パラメータが正しく推定できているかチェック
- 推定結果の解釈
データ取得
物件ごとの家賃と面積などのデータをSUUMOから2023年11月にスクレイピングしました3。
例えば、東京都千代田区の全ての物件は、こちらのページで見ることができます。このページを23区分、PythonのrequestsとBeautifulSoup4を用いてスクレイピングしました。一つの区について、ページネーションを1ページずつめくっていきます。1ページに50件物件が載っているので意外とサクサク取得できます。
数時間かけて129978件の建物における243544件の物件情報を収集しました。ただし、同じ物件が異なる建物名の部屋として重複して登録されていることがあり、その重複を除くと実際には211074件の物件となりました。
Rでスクレイピングしてもよかったですが、Pythonを使ったのは今回はPythonでのクラスや例外処理の勉強を兼ねたためでもあります。rvestも超優秀なパッケージです。
なお、上の一覧ページから各物件の詳細ページに飛ぶと、部屋の設備の有無などの詳細な情報を取得することができます。しかし、このページは物件の数だけページが存在するためにスクレイピングにかかる時間が長くなってしまうのでスクレイピングしていません。前のページが1ページに50件載っているのに対してこちらは1ページに1件なので、こちらも取得しようとするとさらに50倍の時間がかかります。
出力した結果のjsonファイルはこんな感じです。長いので折り畳んでいます。内容はダミーです。建物の数だけ”name”があり、“room”は同一の物件内の部屋の数だけあります。
jsonの中身
[
{
"type": "賃貸マンション",
"name": "hogehogeマンション",
"address": "東京都千代田区千代田1",
"moyorieki": [
"東京メトロ千代田線/大手町駅 歩5分",
"東京メトロ日比谷線/日比谷駅 歩6分",
"JR中央線/東京駅 歩10分"
],
"age": "築1年",
"story": "10階建",
"room": [
{
"floor": "3階",
"rent": "10万円",
"admin": "5000円",
"shikikin": "10万円",
"reikin": "-",
"layout": "ワンルーム",
"area": "25.05m2",
"link": "<物件ページへのリンク>"
},
{
"floor": "5階",
"rent": "12.5万円",
"admin": "10000円",
"shikikin": "12.5万円",
"reikin": "12.5",
"layout": "1LDK",
"area": "50.50m2",
"link": "<物件ページへのリンク>"
}
]
},
{
"type": "賃貸マンション",
(以下同様)
}
]
前処理
ここからはRで行います。
library(tidyverse)
library(rstan)
library(bayesplot)
library(tidybayes)
library(patchwork)
library(furrr)
library(MLmetrics)
上の章で出力したjsonファイルをdata.frameで読み込んでdfという変数に入れておきます。
まず建物名以外が全く同じで建物名のみ異なる物件が結構あります。これは重複とみなしてdplyr::distinct()でレコードを削除しています(32000件程度)。そのうえでいくつかの条件で物件を除外しています。
- 1.1個目の最寄り駅から徒歩ではない物件(バスや車) [1025件]
- 徒歩以外を考慮しようとすると手間がかかるから
- この除外により、最寄駅からバスや車という物件が多い駅の家賃を過大に評価しそうだが今回は単純に除外した
- 2.賃貸マンション、賃貸アパート以外の物件(一戸建てなど)[5392件]
- マンションやアパートとは同列に扱えないから
- 3.物件の階数の情報がない物件 [11件]
- “-”のようなパターン
- 4.物件の階数が建物の地上階の階数より高い物件、または地下階の高さより低い物件
[189件]
- 誤入力?
次に以下のロジックで前処理しました。正規表現とstringrで何とかしました。前処理あるあるなんですが、このコードのロジックで漏れなく前処理できているか?というのを逐一確かめながらコードを書いていくのが大変なんですよね。それでもSUUMOのデータはかなりきれいでした。
ward(区):address(住所)から正規表現で区を抽出area_str(面積): “m2”を削除age_str(築年数): 「築x年」のxを抽出。「新築」なら0、「築99年以上」なら99とするmoyorieki_1(1個目の最寄り駅)から路線部分と駅名部分と徒歩x分のxをそれぞれ別のカラムに入れるrent(家賃),admin(管理費),shikikin(敷金),reikin(礼金)を万円単位で統一する。“-”は0とする- 目的変数である家賃+管理費を
rent_admin(万円)として列を足す story(建物の階数)から地上階数と地下階数をそれぞれstory_aboveとstory_underとして取り出す。平屋は地上1階地下0階建てとするfloor(部屋の階数)から階数を取り出す- 地下階はマイナスを付ける(例: “B2階”は-2とする)
- “1-2階”のような複数階にまたがるものは左側を採用(この例では1階とする)
- “3-1階”のようなパターンもあったが機械的に3階とした
- 適宜double型やinteger型に変換
前処理のコード
df2 <- df |>
# バスや車を除外
filter(str_detect(moyorieki_1, "駅 歩")) |>
filter(!str_detect(moyorieki_1, "駅 バス")) |>
# 「賃貸その他」、「賃貸テラス・タウンハウス」、「賃貸一戸建て」を除外
filter(type %in% c("賃貸マンション", "賃貸アパート")) |>
# 階が入っていないものを除外
filter(floor_str != "-")
df3 <- df2 |>
mutate(
ward=str_extract(address, "(?<=東京都).*?区")
) |>
mutate(
area=as.numeric(str_remove(area, "m2$"))
) |>
mutate(
age=case_when(
age_str == "新築" ~ 0L,
age_str == "築99年以上" ~ 99L,
str_detect(age_str, "^築[0-9]{1,2}年$") ~ as.integer(str_extract(age_str, "(?<=築)[0-9]{1,2}(?=年)"))
)
) |>
mutate(
moyorieki_1_railroad=str_extract(moyorieki_1, "^.*(?=/)"),
moyorieki_1_station=str_extract(moyorieki_1, "(?<=/).*駅"),
moyorieki_1_walk=as.integer(str_extract(moyorieki_1, "(?<=駅 歩).*(?=分)"))
) |>
mutate(
across(
c(rent, admin, shikikin, reikin),
~{
case_when(
.x == "-" ~ 0L,
str_detect(.x, "万円$") ~ as.numeric(str_extract(.x, "[0-9\\.]+(?=万円$)")),
str_detect(.x, "(?!=万)円$") ~ as.numeric(str_extract(.x, "[0-9\\.]+(?=円$)"))/10000
)
}
),
rent_admin=rent + admin
) |>
mutate(
story_above=case_when(
str_detect(story_str, "(?<=地上)[0-9]+(?=階建$)") ~ as.integer(str_extract(story_str, "(?<=地上)[0-9]+(?=階建$)")),
str_detect(story_str, "[0-9]+階建$") ~ as.integer(str_extract(story_str, "[0-9]+(?=階建$)")),
story_str == "平屋" ~ 1L
),
story_under=case_when(
str_detect(story_str, "(?<=^地下)[0-9]+") ~ as.integer(str_extract(story_str, "(?<=^地下)[0-9]+")),
story_str == "平屋" ~ 0L,
TRUE ~ 0L
)
) |>
mutate(
floor=case_when(
str_detect(floor_str, "^B[0-9]+階$") ~ as.integer(str_extract(floor_str, "[0-9]+")) * -1L,
floor_str == "B階" ~ -1L,
str_detect(floor_str, "B\\-.*階") ~ -1L,
str_detect(floor_str, "^[0-9]+階$") ~ as.integer(str_extract(floor_str, "[0-9]+")),
str_detect(floor_str, "^B[0-9]+\\-[BM]?[0-9]+階$") ~ as.integer(str_extract(floor_str, "(?<=B)[0-9]+")) * -1L,
str_detect(floor_str, "^[0-9]+\\-[BM]?[0-9]+階$") ~ as.integer(str_extract(floor_str, "^[0-9]+"))
)
)
df4 <- df3 |>
filter(floor >= story_under * -1, floor <= story_above) |>
select(
-moyorieki_1, -moyorieki_2, -moyorieki_3,
-age_str, -story_str, -floor_str,
-shikikin, -reikin
)
これをdf4として格納します。次の画像のようなdata.frameです。結果として204457件の物件が残りました。
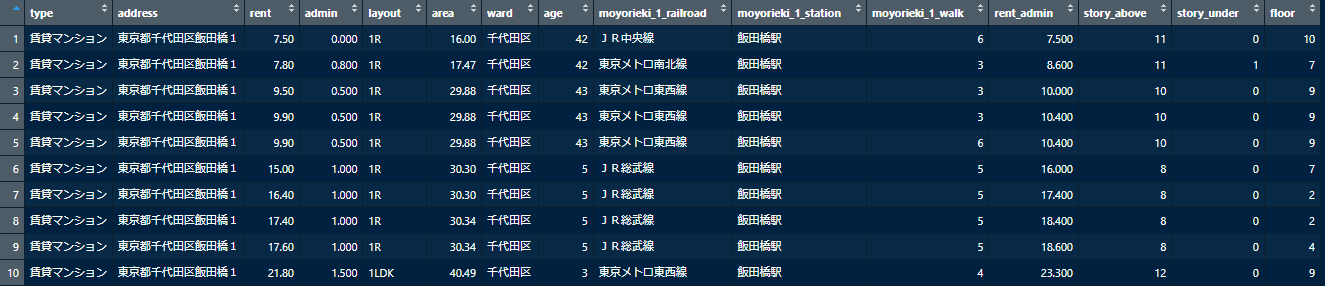
可視化
ようやくきれいなテーブルデータができたので、ggplot2で色々プロットしてみます。
探索的データ分析の過程ではデュアルディスプレイの片面にRStudioとかVSCodeとかのIDE、もう片面にプロットを表示すると快適です。
間取り・面積の分布
1つの建物に3つの部屋の募集が掲載されていたら、物件数は3とカウントします。また、面積は150m2以上は150m2として扱います。
Code
p1 <- df4 |>
count(layout, name="count") |>
arrange(desc(count)) |>
ggplot(aes(forcats::fct_reorder(layout, count), count))+
theme_light()+
geom_bar(stat="identity", alpha=0.6, color="black")+
labs(x="layout(間取り)", y="物件数(部屋)")+
coord_flip()
p2 <- df4 |>
mutate(area=if_else(area >= 150, 150, area)) |>
ggplot(aes(area))+
theme_light()+
geom_histogram()+
scale_x_continuous(breaks=seq(0, 150, 50), minor_breaks=seq(0, 150, 10))+
labs(x="area(面積)", y="物件数(部屋)")
patchwork::wrap_plots(p1, p2, ncol=2)
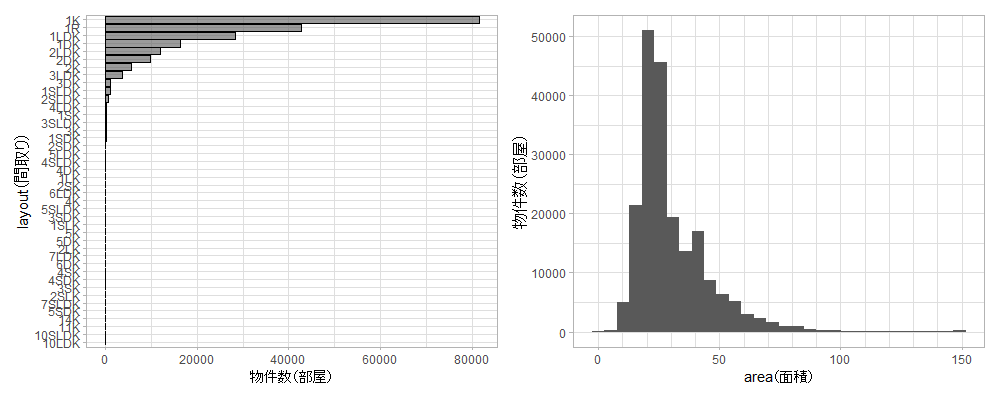
11Kや14Kは1Kの誤入力でした。20m2~50m2あたりのゾーンがボリュームゾーンなんですね。
家賃・築年数の分布
左の家賃のグラフですが、外れ値でプロットが見づらくなるので家賃100万円以下の物件のみに絞ります。
Code
p1 <- df4 |>
ggplot(aes(rent_admin))+
theme_light()+
geom_histogram(binwidth=2)+
coord_cartesian(xlim=c(0, 100))+
scale_x_continuous(breaks=seq(0, 100, 10), minor_breaks=NULL)+
labs(x="rent_admin(家賃+管理費)", y="物件数(部屋)")
p2 <- df4 |>
ggplot(aes(age))+
theme_light()+
geom_histogram()+
scale_x_continuous(breaks=seq(0, 100, 10), minor_breaks=NULL)+
labs(x="age(築年数)", y="物件数(部屋)")
patchwork::wrap_plots(p1, p2, ncol=2)
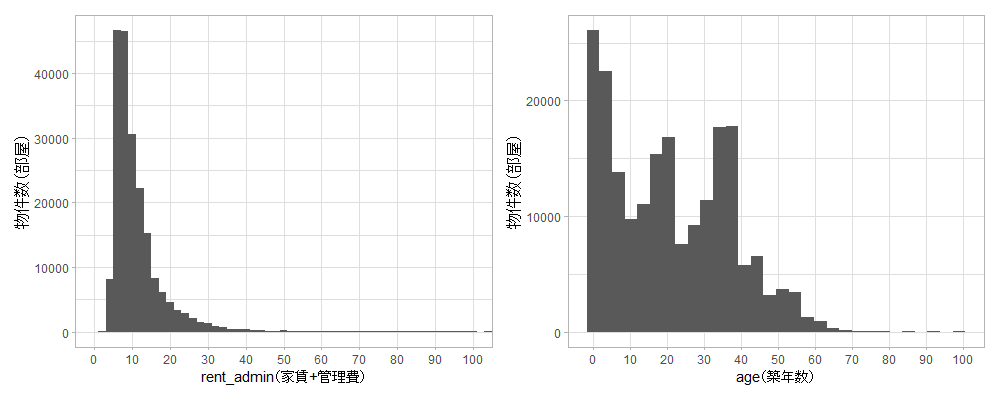
家賃の分布は右に裾を引いた対数正規分布のような形をしています。
右の築年数の分布は20年と40年手前に崖があります。建物が満たすべき耐震基準は建築基準法で定められており、1981年以前に建築確認申請が行われた建物は「旧耐震基準」、それ以降の建物は「新耐震基準」、2000年以降の建物は「2000年基準」が適用されるそうです。後ろほど耐震基準が高まります。新耐震基準適用開始から40年、2000年基準適用開始から20年くらいになるので、20年や40年を目途に建て替えられているのかもしれません(建築は特に詳しくないので違うかもしれません。単なる推測です)。
面積と家賃の散布図(間取りで色分け)
点の色分けが分かりづらくなるので、1R, 1K, 1DK, 1LDK, 2K, 2DK, 2LDK以外の間取りをothersにまとめています。また、面積100m2以下、家賃50万円以下の物件のみをプロットします。
Code
df4 |>
mutate(
layout=if_else(layout %in% c("1K", "1R", "1LDK", "1DK", "2LDK", "2DK", "2K"), layout, "others")
) |>
ggplot(aes(area, rent_admin, color=layout))+
theme_light()+
geom_point(size=0.1)+
coord_cartesian(xlim=c(0, 100), ylim=c(0, 50))+
guides(colour=guide_legend(override.aes=list(size=6)))+
labs(x="area(面積)", y="rent_admin(家賃+管理費)")
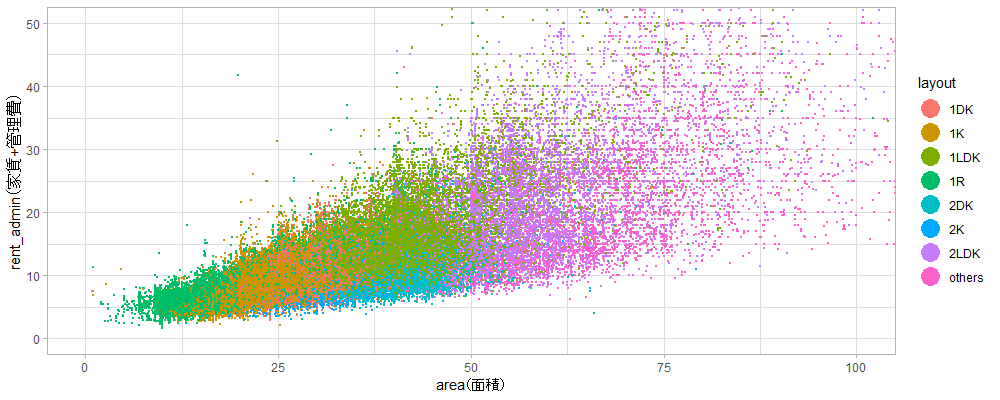
面積が小さい方から1R(緑色)、1K(黄土色)、1DK(オレンジ色)、1LDK(黄緑色)、2LDK(紫色)は同じ直線に乗っているように見えます。つまり、これらの5個の間取りに関しては、面積と間取りは相関が非常に高く多重共線性を起こしそうなことを示します。
一方でちょっと見づらいですが、2K(青色)は1K~1DKと同じ面積なのに下の方に位置するように見えます。同じく2DK(水色)も1LDKと同じ面積なのに下の方にあります。
この理由は次のプロットで推測できます。
築年数の分布(間取り別)
上の散布図と同じデータを、築年数のヒストグラムで描きます。
Code
df4 |>
mutate(
layout=if_else(layout %in% c("1K", "1R", "1LDK", "1DK", "2LDK", "2DK", "2K"), layout, "others")
) |>
ggplot(aes(age))+
theme_light()+
geom_histogram()+
labs(x="age(築年数)", y="物件数(部屋)")+
theme(
strip.background=element_rect(color="black", fill="white"),
strip.text=element_text(color="black")
)+
facet_wrap(~layout, ncol=4)
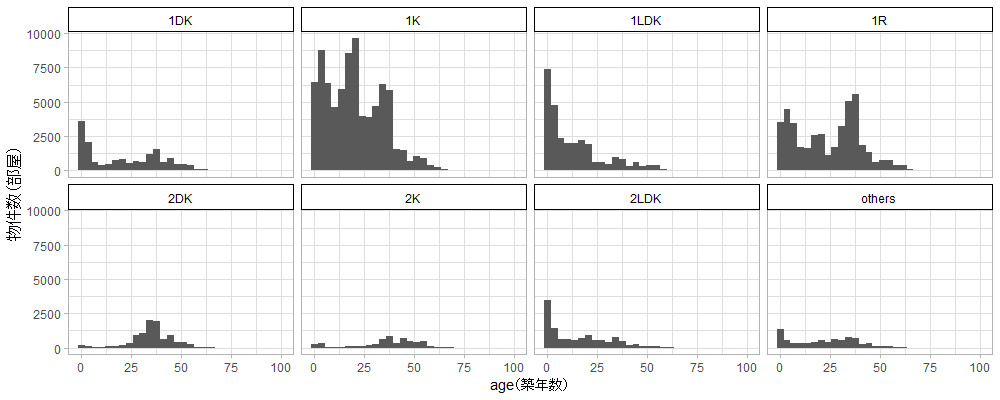
すると、2Kと2DKは他の間取りと違い、築年数が25年~50年の間にピークがあることが分かります。
つまり、一つ前の面積と家賃の散布図における、「2Kは1Kや1DKと同じ面積なのに下の方に位置し、同様に2DKは1LDKと同じ面積なのに下の方に位置する」現象は、2Kと2DKは築年数が経過した物件が多いため、2Kは1Kや1DK、2DKは1LDKと同じ面積でも家賃が安いということだと推測できます。そうなら、間取りは説明変数から削除してもよさそうです。
以下のページにもあるのですが、間取りにも流行りがあるそうです。
- 【ホームズ】お得に部屋を借りたい人は「2K」も視野に!ワンルームより家賃が安いことも | 住まいのお役立ち情報
- 1LDKと2DKはどっちが安い?間取りの違いとおすすめな人もご紹介 | CHINTAI情報局
面積と家賃の散布図(築年数別・徒歩分数別)
上で見た面積と家賃のプロットを150m2以下、200万円以下に広げて築年数で色分けしてみます。グラデーションを見やすくするため、築年数が40年以上は40年としています。右のプロットは面積と家賃を両方対数を取ったものです。
Code
p1 <- df3 |>
filter(area <= 150 & rent_admin <= 200) |>
mutate(age=if_else(age >= 40L, 40L, age)) |>
ggplot(aes(area, rent_admin, color=age))+
theme_light()+
geom_point(size=0.1)+
theme(legend.position="bottom")+
labs(x="area(面積)", y="rent_admin(家賃+管理費)")+
geom_vline(xintercept=10, color="purple")+
geom_vline(xintercept=100, color="black")+
geom_hline(yintercept=100, color="firebrick")
p2 <- df3 |>
filter(area <= 150 & rent_admin <= 200) |>
mutate(age=if_else(age >= 40L, 40L, age)) |>
ggplot(aes(log(area), log(rent_admin), color=age))+
theme_light()+
geom_point(size=0.1)+
theme(legend.position="bottom")+
labs(x="log(area)(面積の対数)", y="log(rent_admin)(家賃+管理費の対数)")+
geom_vline(xintercept=log(10), color="purple")+
geom_vline(xintercept=log(100), color="black")+
geom_hline(yintercept=log(100), color="firebrick")
patchwork::wrap_plots(p1, p2, ncol=2)
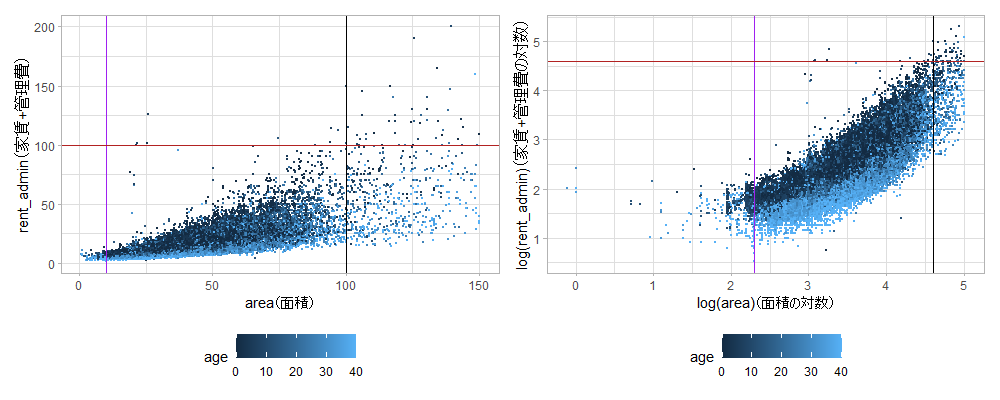
x=10, x=100, y=100にそれぞれ紫色、黒色、赤色の線を引いています。
右側の両対数プロットだと、築年数が増えるほど点が下方にシフトしているように見えますね。
左のプロットを見ると、面積が100m2(黒色の線)を超えるあたりからばらつきが大きくなっています。100m2を超える広い物件は家賃のメカニズムも変わってきそうです。23区で100m2のマンションはかなり広いです。面積がかなり大きいゾーンにも当てはめようとすると、ボリュームゾーンの25m2~50m2の物件の当てはまりが悪くなりそうなので、100m2を超える物件はモデルから除外することにします。また、100m2超はデータの誤入力っぽい物件もちらほらあるので、それを弾く意味もあります。
100m2以下の物件はほとんど100万円(赤色の線)以下に収まっていますね。いま、モデルには100m2以下の物件データのみを使うことにしたので、誤入力をはじく意味で家賃が100万円の物件も除外することにします。
また、右の対数のプロットを見ると、10m2(紫色の線)より左側は線形の関係が成り立っていなさそうです。このような狭い物件にも対数線形のモデルをフィットさせようとするのはやはり難しそうなので、10m2以下の物件も除外します。
次のプロットは、先ほどのプロットの色分けを最寄り駅からの徒歩分数にしたものです。ただし20分以上は20分にまとめています。
Code
p1 <- df3 |>
filter(area <= 150 & rent_admin <= 200) |>
mutate(moyorieki_1_walk=if_else(moyorieki_1_walk >= 20L, 20L, moyorieki_1_walk)) |>
ggplot(aes(area, rent_admin, color=moyorieki_1_walk))+
theme_light()+
geom_point(size=0.1)+
theme(legend.position="bottom")+
labs(x="area(面積)", y="rent_admin(家賃+管理費)")+
geom_vline(xintercept=10, color="purple")+
geom_vline(xintercept=100, color="black")+
geom_hline(yintercept=100, color="firebrick")
p2 <- df3 |>
filter(area <= 150 & rent_admin <= 200) |>
mutate(moyorieki_1_walk=if_else(moyorieki_1_walk >= 20L, 20L, moyorieki_1_walk)) |>
ggplot(aes(log(area), log(rent_admin), color=moyorieki_1_walk))+
theme_light()+
geom_point(size=0.1)+
theme(legend.position="bottom")+
labs(x="log(area)(面積の対数)", y="log(rent_admin)(家賃+管理費の対数)")+
geom_vline(xintercept=log(10), color="purple")+
geom_vline(xintercept=log(100), color="black")+
geom_hline(yintercept=log(100), color="firebrick")
patchwork::wrap_plots(p1, p2, ncol=2)
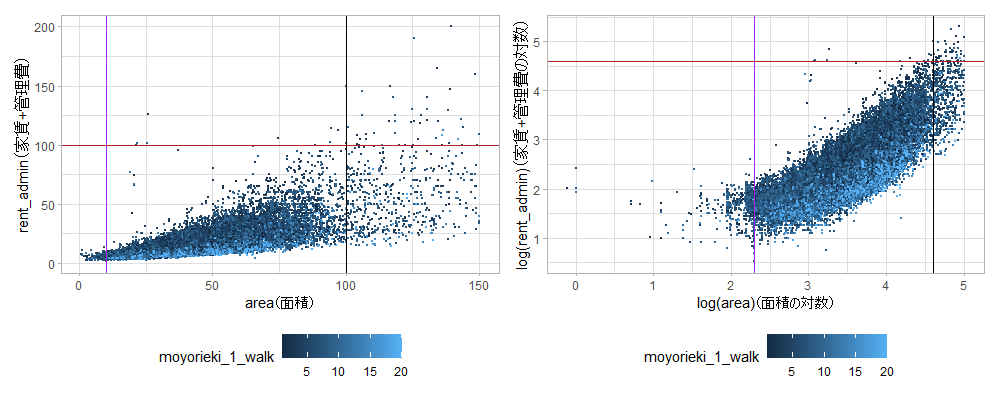
築年数と同様、徒歩分数が増えると点が下方にシフトしているように見えます。これは、対数家賃を対数面積で回帰するモデルを組むと、築年数と徒歩分数はこの回帰式の項に加えられることを示唆します。
面積と家賃の散布図(最寄り駅別・築年数で色分け)
23区の各区ごとに最も物件数が多い最寄り駅の物件について、築年数で色分けして面積と家賃の散布図を描いてみます。グラデーションを見やすくするため、築年数が40年以上は40年としています。面積は100m2以下、家賃は50万円以下に絞っています。
Code
top_stations_in_each_ward <- df4 |>
count(ward, moyorieki_1_station, name="n") |>
group_by(ward) |>
mutate(rank=dense_rank(desc(n))) |>
filter(rank == 1) |>
pull(moyorieki_1_station)
df4 |>
filter(moyorieki_1_station %in% top_stations_in_each_ward) |>
mutate(age=if_else(age >= 40L, 40L, age)) |>
ggplot(aes(area, rent_admin, color=age))+
theme_light()+
geom_point(size=1)+
coord_cartesian(xlim=c(0, 100), ylim=c(0, 50))+
labs(x="area(面積)", y="rent_admin(家賃+管理費)")+
theme(
strip.background=element_rect(color="black", fill="white"),
strip.text=element_text(color="black")
)+
facet_wrap(~moyorieki_1_station, ncol=4)
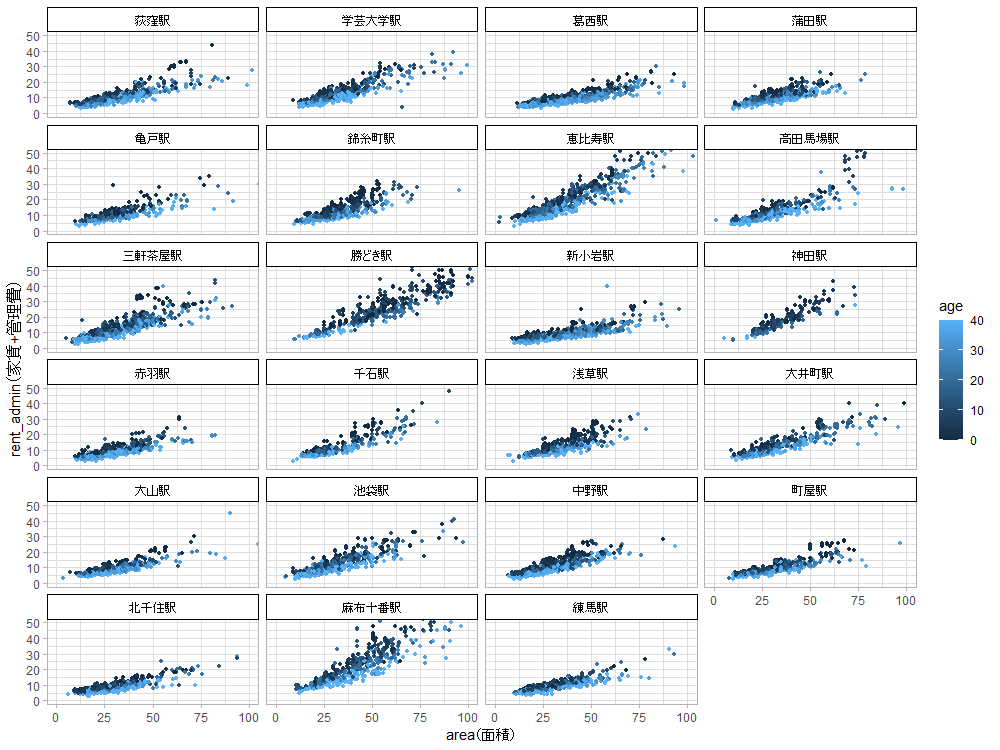
恵比寿と麻布十番は高いですね。神田や勝どきも高いし、濃い色の点が多いので築浅物件が多そうです(実際、駅別に築年数のヒストグラムを描くとその通りです)。
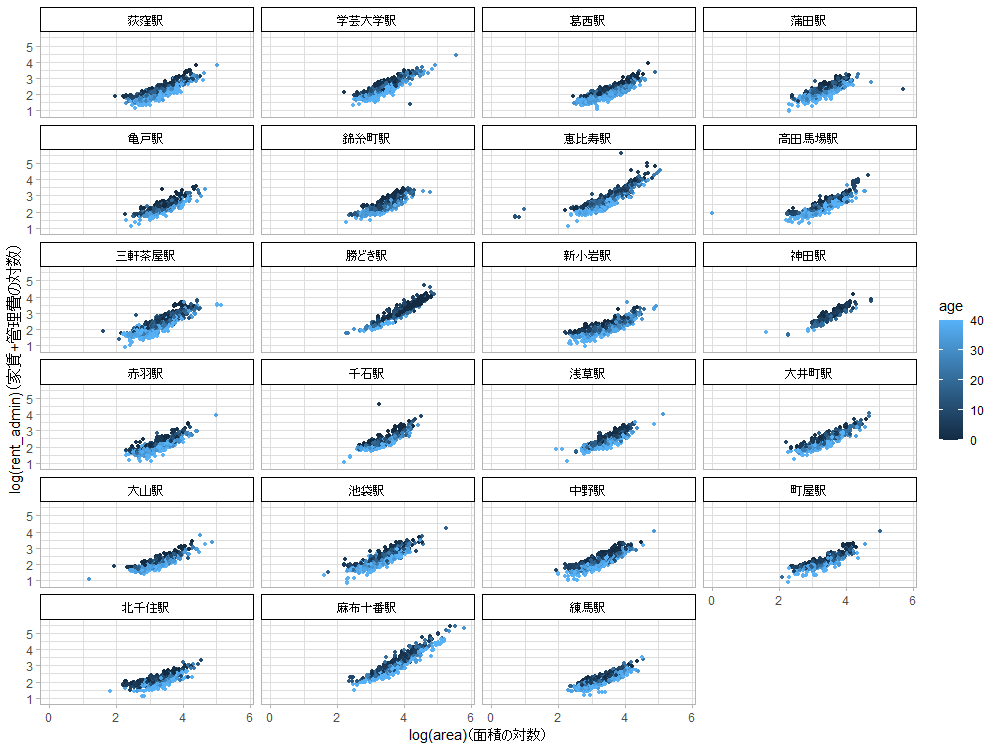
次のプロットで面積と家賃をそれぞれ自然対数を取って描き直してみると、駅によって面積と家賃の傾きが違う直線に乗り、また対数を取る前より面積が大きいゾーン(x軸の右の方)のばらつきが抑えられたことが分かります。
Code
df4 |>
filter(moyorieki_1_station %in% top_stations_in_each_ward) |>
mutate(age=if_else(age >= 40L, 40L, age)) |>
ggplot(aes(log(area), log(rent_admin), color=age))+
theme_light()+
geom_point(size=1)+
labs(x="log(area)(面積の対数)", y="log(rent_admin)(家賃+管理費の対数)")+
theme(
strip.background=element_rect(color="black", fill="white"),
strip.text=element_text(color="black")
)+
facet_wrap(~moyorieki_1_station, ncol=4)
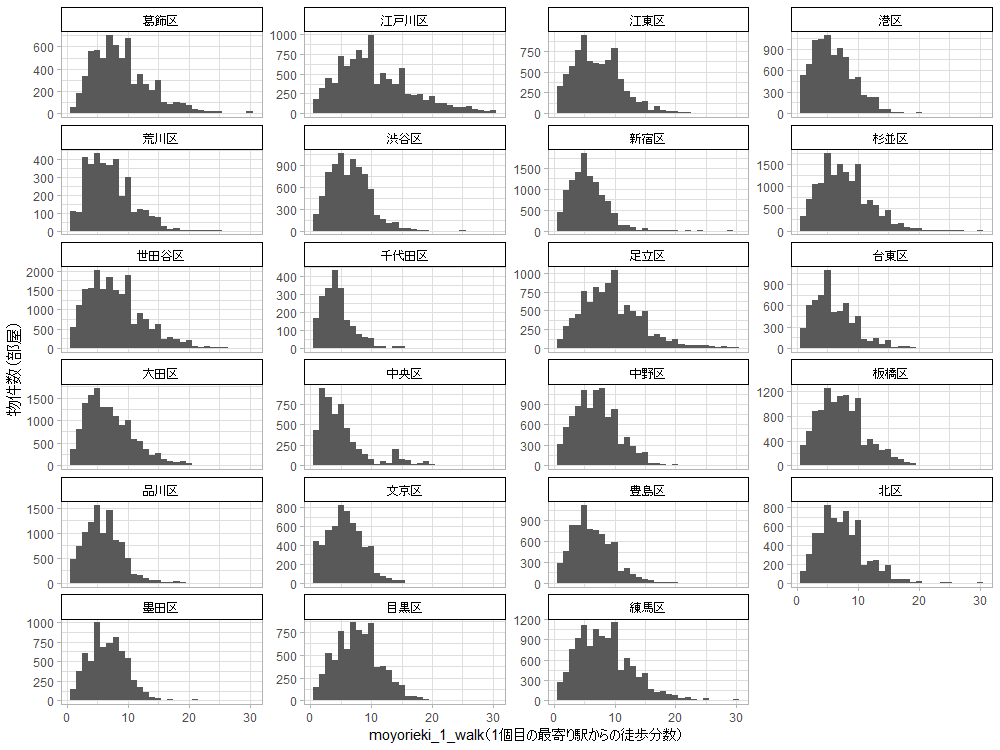
徒歩分数の分布
1個目の最寄り駅(物件ページの一番上に書いてある最寄り駅)からの徒歩分数の1分刻みのヒストグラムです。ただし30分以上の場合は30分としています。
5分と10分が多く見えます。物件サイトで検索するときは駅から5分以内や10分以内でフィルターをかけて検索することが多いので、駅から10分以上かかるような最寄り駅と駅からギリギリ10分という最寄り駅があったら、後者を最寄り駅として書くのかもしれません。
Code
df4 |>
mutate(moyorieki_1_walk=if_else(moyorieki_1_walk >= 30L, 30L, moyorieki_1_walk)) |>
ggplot(aes(moyorieki_1_walk))+
theme_light()+
geom_histogram(binwidth=1)+
labs(x="moyorieki_1_walk(1個目の最寄り駅からの徒歩分数)", y="物件数(部屋)")+
theme(
strip.background=element_rect(color="black", fill="white"),
strip.text=element_text(color="black")
)+
facet_wrap(~ward, ncol=4, scales="free_y")
モデリング
モデルの設計
長かったですが、可視化の結果とドメイン知識を踏まるとこんな感じです。改めてですが、断りがない限り「家賃」は「家賃+管理費」を指します。
- 横軸を面積、縦軸を家賃に取ると、最寄り駅によって切片と傾きが違う
- 面積と間取りは家賃に与える情報が被りそう
- 築年数や徒歩分数が増えるほど家賃は下がる
2つ目はちょっとだけ意外かもしれませんが、そりゃそうだよねという感じです。可視化の結果誰も知らないことが分かることはあまりなく、えてして皆が知っていることをデータから再確認するものなのです。
同じ面積でも最寄り駅によって家賃は違いそうです。また、面積が2倍になればある最寄り駅の物件では家賃が1.5倍になるかもしれないし、ある最寄り駅では3倍になるかもしれないですね。
築年数は1年増えるごとに、徒歩分数は1分増えるごとに定数が乗算されて家賃が下がるモデルにしてみます。つまり新築で10万円の物件なら築5年で9万円、築10年で8万円として、新築で20万円の物件なら築5年で18万円、築10年なら16万円というイメージでしょう。家賃の絶対水準が違うからですね。
これは築年数や徒歩分数は家賃の対数に対して負の線形の関係があるということです。特に築年数に関して言うと、建物は一年あたりの減価率の年数乗で減価するというのは直感(ドメイン知識)と合っています。減価償却の定率法的な感じです。
ここまで書いたことを以下のようにモデルで表現してみました。
物件$i(1, \dots, N)$の最寄り駅(SUUMOの物件ページで一番上に書いてある1番目の最寄り駅)を$sta[i] (1, \dots, S)$とします。
$$ \begin{align*} \log{y_{i}} & \sim N(\mu_{i}, \sigma) \\\ \mu_{i} &= a_{sta[i]} + b_{sta[i]} \log{\mathrm{area}_{i}} \\\ &+ \beta_{\mathrm{age}} \mathrm{age}_{i} + \beta_{\mathrm{walk}}(\mathrm{walk}_{i} - 1) \\\ a_{sta[i]} & \sim N(a_{all}, \sigma_{a_{all}}) \\\ b_{sta[i]} & \sim N(b_{all}, \sigma_{b_{all}}) \\\ \end{align*} $$
ただし、物件$i$について、それぞれ以下の通りとします。
- $y_{i}$: 家賃+管理費(万円)
- $\mathrm{area}_{i}$: 面積(m2)
- $\mathrm{age}_{i} (0 \leq \mathrm{age}_{i} \leq 40)$: 築年数(年、整数)。新築は0年とする
- $\mathrm{walk}_{i} (1 \leq \mathrm{walk}_{i} \leq 20)$: 最寄り駅からの徒歩分数(分、整数)。徒歩0分という物件はない
最寄り駅が$sta[i]$, 面積が$\mathrm{area}_{i}$(m2), 築年数が$\mathrm{age}_{i}$(年), 最寄り駅から徒歩$\mathrm{walk}_{i}$(分)の物件$i$について、その家賃(管理費込み)の対数$\log{y_{i}}$(万円)は、平均$\mu_{i}$, 標準偏差$\sigma$の正規分布に従うと仮定したモデルです。ただし、最寄り駅が複数あっても1個しか考慮しません。要するに物件の最寄り駅で階層化した面積のランダム切片+ランダム係数モデルに、築年数と最寄り駅からの徒歩分数による減価要素を入れたものです。
このとき、この最寄り駅、面積、築年数、徒歩分数での条件における物件の対数家賃の相場は$\mu_{i}$万円であると考えます。
最寄り駅ごとに回帰直線を別々に推定するのではなく階層モデルにすると何がうれしいのかというと、サンプル数の少ない駅でも全体の傾向を借用してパラメータを推定することができます。これを縮約といいます。また、各最寄り駅のパラメータ$a_{sta[i]}, b_{sta[i]}$は、$a_{all}, b_{all}$という全ての最寄り駅の「平均的な」パラメータから$\sigma_{a_{all}}, \sigma_{b_{all}}$だけばらつくという、ドメイン知識に合ったメカニズムを組み込むことができるのもメリットです。
なお、$y_{i}$と$area_{i}$は対数変換しない選択肢もありますが、いま定式化したように、家賃 + 管理費 = (a + b * 面積) * 築年数効果 * 徒歩分数効果という右辺が乗算のモデルを考えるなら、左辺を対数変換すると右辺を加算の関係に変換することができるので、StanでのMCMCが収束しやすいというメリットもあります。a*築年数効果のようなパラメータ同士の積があると収束しにくいです。
モデルに投入するデータ
投入するデータは、SUUMOに掲載されている東京23区のデータのうち、以下を除外した178113件のデータです。
- 1.1個目の最寄り駅から徒歩ではない物件(バスや車) [1025件]
- 2.賃貸マンション、賃貸アパート以外の物件(一戸建てなど)[5392件]
- 3.物件の階数の情報がない物件 [11件]
- 4.物件の階数が建物の地上階の階数より高い物件、または地下階の高さより低い物件 [189件]
- 5.家賃+管理費が100万円を超える物件 [1286件]
- 6.面積が100m2を超える物件 [436件]
- 7.面積が10m2未満の物件 [1033件]
- 8.築年数が40年を超える物件 [22565件]
- 40年超の物件は数が減るため
- 9.1個目の最寄り駅からの徒歩分数が20分を超える物件 [1852件]
- 8と同様
1~4は可視化の時点で既に除外していました。5~9は可視化の結果を踏まえてモデルの推定では追加で除外することにしました。
徒歩分数の方はともかく築年数の方は全体の1割なので少なくはないですが、今回は築年数が40年まで見られれば自分の関心を満たせるということでいったん40年で切りました。可視化の章で述べた通り40年を目安に適用される建築基準法が異なる問題もあるので、家賃相場の傾向も変わってくる可能性があります。40年で分けて考えるのは悪くなさそうです。
Stanの実装
以下のコードです。
data {
int N; // 物件の数
vector[N] Y; // 物件nの家賃+管理費
vector[N] AREA; // 物件nの面積
int S; // 最寄り駅の数
int<lower=1, upper=S> STATION[N]; // 物件nの最寄り駅index
vector[N] AGE; // 物件nの築年数(lower=0, upper=40の整数)
vector[N] WALK; // 物件nの徒歩分数(lower=1, upper=20の整数)
}
parameters {
real a0; // 面積の切片の全体平均
real b0; // 面積の傾きの全体平均
vector[S] a;
vector[S] b;
real<upper=0> age_b;
real<upper=0> walk_b;
real<lower=0> sigma_a;
real<lower=0> sigma_b;
real<lower=0> sigma; // 物件ごとのばらつき
}
model {
// 最寄り駅による面積の階層効果
a ~ normal(a0, sigma_a);
b ~ normal(b0, sigma_b);
log(Y) ~ normal(a[STATION] + b[STATION] .* log(AREA) + age_b*AGE + walk_b*(WALK - 1), sigma);
}
事前分布は無情報事前分布です。
全体平均のa0とb0を正規分布の平均として織り込むというのは階層モデルのMCMC推定の高速化と収束しやすくするテクニックです。アヒル本(StanとRでベイズ統計モデリング)の8.1.6章を参考にしました。
高速化のためにベクトル化しているので少し分かりづらいですが、ベクトル化しないと以下のコードです。
model {
for (s in 1:S) {
a[s] ~ normal(a0, sigma_a);
b[s] ~ normal(b0, sigma_b);
}
for (n in 1:N) {
log(Y[n]) ~ normal(a[STATION[n]] + b[STATION[n]]*log(AREA[n]) + age_b*AGE[n] + walk_b*(WALK[n] - 1), sigma);
}
}
このコードを”model.stan”で保存して以下のRコードでキックします。chains=4, iter=5000, warmup=1000で約12時間かかりました。
Code
# 特徴量生成
df_mod <- df4 |>
filter(rent_admin <= 50 & area <= 100) |>
filter(moyorieki_1_walk <= 20 & age <= 40) |>
# Stanに渡すために最寄り駅 (character) をfactorを経由してintegerにする
mutate(moyorieki_1_station_index=as.integer(as.factor(moyorieki_1_station)))
# 上はMCMCの並列化、下はstanコードが変わらない限り再コンパイルしない
options(mc.cores=parallel::detectCores())
rstan::rstan_options(auto_write=TRUE)
# Stanコードのコンパイル
mod <- rstan::stan_model("model.stan")
# MCMCの実行
fit <- rstan::sampling(
mod,
data=list(
N=nrow(df_mod),
Y=df_mod$rent_admin,
AREA=df_mod$area,
S=length(unique(df_mod$moyorieki_1_station_index)),
STATION=df_mod$moyorieki_1_station_index,
AGE=df_mod$age,
WALK=df_mod$moyorieki_1_walk
),
chains=4, iter=5000, warmup=1000, thin=1, refresh=10, seed=1234
)
デフォルトではiter/10ごとにprogressが出力されますが、MCMCの推定に時間がかかるようなモデルの場合は中々出力されず不安になるのでrefreshに小さい値を指定しておくことで細かくprogressを表示しておくといいです。
推定結果のチェック
MCMCのチェック
StanのMCMCが終わったら、パラメータが正しく推定されていることを確かめるために、以下をチェックします。bayesplotを使うと簡単にプロットできます。
- トレースプロットが混ざり合っていること
- MCMCで生成されたパラメータのサンプルが初期値によらず同じ値に収束しているか(=局所解に落ちていないか)の確認
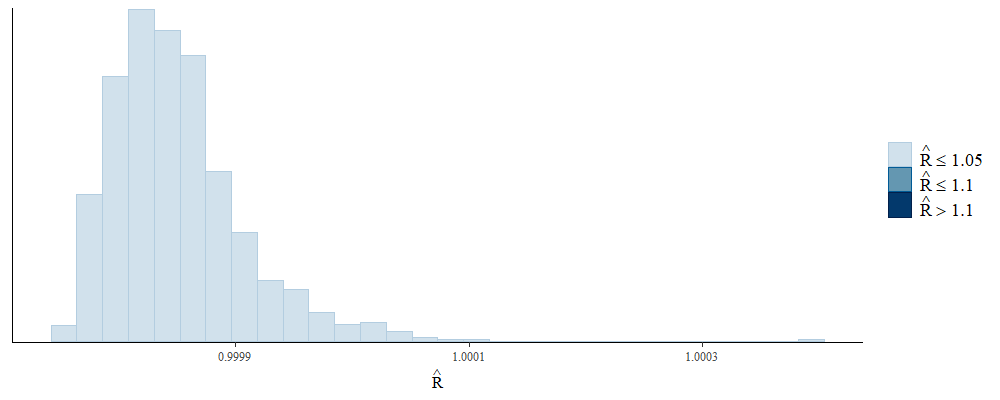
- Rhat < 1.1であること
- 上の収束の度合いを数値で表したもの
- 有効サンプルサイズn_effが大きいこと
- サンプルが互いに独立であることを示す(=定常な分布に収束している)
- 目安はサンプル数で割った値が0.1以上
- パラメータのサンプルに自己相関がないこと
- 上を自己相関係数のプロットで示したもの
事後診断の詳細はこちらの素晴らしい記事も参考にさせていただきました。
[R] [stan] bayesplot を使ったモンテカルロ法の実践ガイド - ill-identified diary
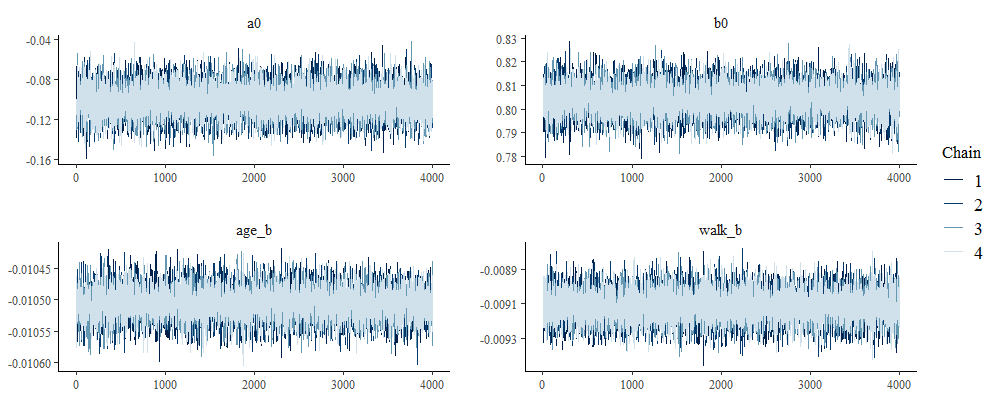
以下にプロットを載せます。きれいなプロットで全てよさそうです。
スペース的に全部のパラメータを載せることは難しいのでトレースプロット(1枚目)と自己相関(4枚目)で描くパラメータは一部のパラメータに絞っていますが、他のパラメータも問題ありませんでした。
# トレースプロット
bayesplot::mcmc_trace(fit, pars=c("a0", "b0", "age_b", "walk_b"))
# Rhatのヒストグラム
bayesplot::mcmc_rhat_hist(bayesplot::rhat(fit))
# n_eff/Nのヒストグラム
bayesplot::mcmc_neff_hist(bayesplot::neff_ratio(fit))
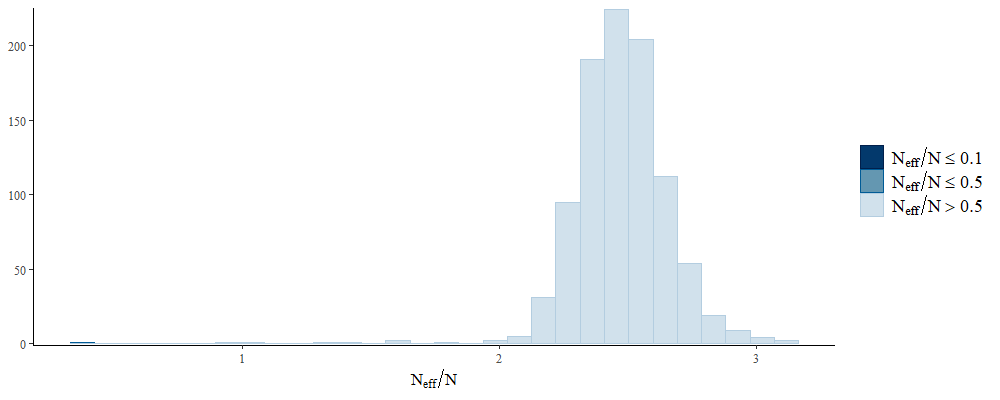
# 自己相関係数のプロット
bayesplot::mcmc_acf_bar(fit, pars=c("a0", "b0", "age_b", "walk_b"))
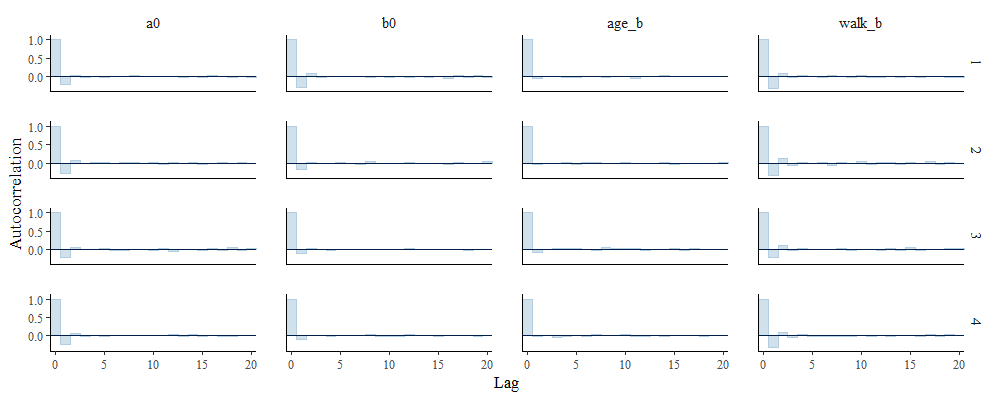
モデルの当てはまりのチェック
MCMCのサンプリングがうまく収束したことは分かりましたが、そもそも今回設定したモデルは現実の家賃データに当てはまっているのか?ということを確かめます。
これは、Stanのgenerated quantitilesブロックに以下のように書いてStan上で予測値を生成すればいいです。
generated quantities {
vector[N] y_pred;
for (n in 1:N) {
y_pred[n] ~ exp(normal_rng(a[STATION[n]] + b[STATION[n]] * log(AREA[n]) + age_b*AGE[n] + walk_b*(WALK[n] - 1), sigma));
}
}
しかし、N=18万弱のy_predそれぞれについて、(5000 (iter) - 1000 (warmup)) / 1 (thin) * 4 (chain) = 16000個(draw)の予測値をStanで生成するため、rstan::extract(fit)$y_predは16000
x
18万弱のmatrixとなります。これではrstan::sampling()の返り値はとんでもなく大きいサイズのオブジェクトになってしまいます。
大まかな事後予測チェックには予測値はそんなにたくさんなくてもいいと思い、Stanで上のコードを書くのではなく、Rでパラメータの事後分布からサンプリングして予測値を100個生成することにしました。要するに100
x
18万弱のmatrixを作る(このサイズのmatrixでも150MBあります)ということです。(Stanコードでgenerated quantitiesの予測値をdraw個ではなく100個など任意の個数に絞る方法はあるのでしょうか…)
furrrで並列化して10秒くらいで生成できました。
Code
# MCMCのサンプルを取り出す
# matrix (draws x stations)
sample_a <- rstan::extract(fit, "a")$a
sample_b <- rstan::extract(fit, "b")$b
# vector (length = draws)
sample_age_b <- rstan::extract(fit, "age_b")$age_b
sample_walk_b <- rstan::extract(fit, "walk_b")$walk_b
sample_sigma_a <- rstan::extract(fit, "sigma_a")$sigma_a
sample_sigma_b <- rstan::extract(fit, "sigma_b")$sigma_b
sample_sigma <- rstan::extract(fit, "sigma")$sigma
# 予測値の中央値を求める関数(n_pred個の予測値を作る)
calc_pred <- function(station_idx, area, age, walk, n_pred, seed) {
mu <- sample_a[,station_idx] + sample_b[,station_idx]*log(area) + sample_age_b*age + sample_walk_b*(walk - 1)
mu2 <- withr::with_seed(seed, sample(mu, size=n_pred))
sigma2 <- withr::with_seed(seed, sample(sample_sigma, size=n_pred))
map2_dbl(mu2, sigma2, function(x, y) {
withr::with_seed(seed, rnorm(1, mean=x, sd=y))
})
}
station_idxs <- df_mod$moyorieki_1_station_index
areas <- df_mod$area
ages <- df_mod$age
walks <- df_mod$moyorieki_1_walk
rent_admins <- df_mod$rent_admin
variables <- list(
station_idx=station_idxs,
area=areas,
age=ages,
walk=walks
)
# 予測値を求める
future::plan(future::multisession)
y_preds <- furrr::future_pmap(
variables,
function(station_idx, area, age, walk) {
calc_pred(station_idx, area, age, walk, n_pred=100, seed=1234)
},
.progress=TRUE,
.options=furrr::furrr_options(seed=1234)
)
# bayesplotに渡すためにsample (n_pred) x data length (180000)のmatrixに変換する
y_pred <- simplify2array(y_preds)
以下は調整済みではない決定係数です。1個目の結果は家賃の対数との比較、2個目は対数ではない家賃との比較です。trainとtestのsplitはしていないので、学習データ内での決定係数です。予測値を100個しか作っていないので参考程度ですが、0.91程度なので悪くないでしょう。
MLmetrics::R2_Score(apply(y_pred, 2, median), log(rent_admins))
#> [1] 0.9294308
MLmetrics::R2_Score(apply(exp(y_pred), 2, median), rent_admins)
#> [1] 0.9082848
次は予測値(横軸)と実際の値(縦軸)のプロットです。左のプロットは対数家賃、右は対数を外した家賃です。
Code
patchwork::wrap_plots(
bayesplot::ppc_scatter_avg(log(rent_admins), y_pred, size=0.1)+
geom_abline(slope=1, intercept=0)+
labs(title="対数家賃"),
bayesplot::ppc_scatter_avg(rent_admins, exp(y_pred), size=0.1)+
geom_abline(slope=1, intercept=0)+
labs(title="家賃"),
ncol=2
)
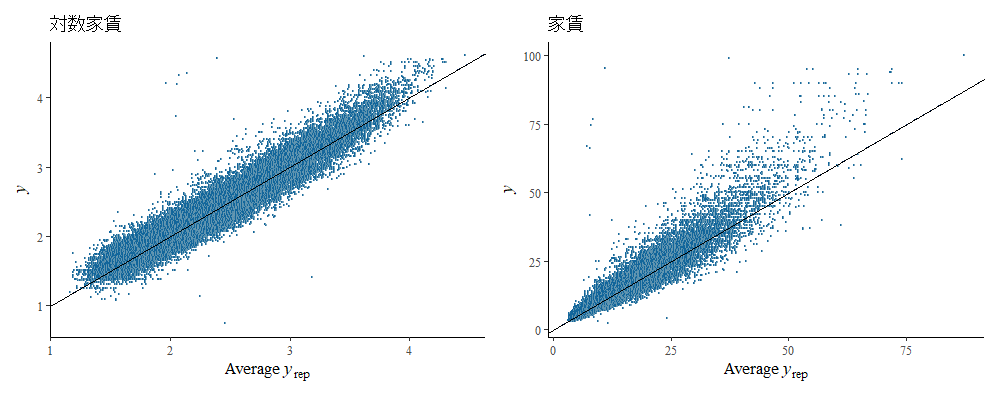
左の対数家賃が45度線上に載っています。
次は残差のプロットです。横軸は面積、縦軸は残差(予測値-実際の値)です。
Code
patchwork::wrap_plots(
bayesplot::ppc_error_scatter_avg_vs_x(log(rent_admins), y_pred, df_mod$area, size=0.1)+
labs(title="対数家賃")+
geom_vline(xintercept=0)+
scale_y_continuous(breaks=seq(0, 100, 20)),
bayesplot::ppc_error_scatter_avg_vs_x(rent_admins, exp(y_pred), df_mod$area, size=0.1)+
labs(title="家賃")+
geom_vline(xintercept=0)+
scale_y_continuous(breaks=seq(0, 100, 20)),
ncol=2
)
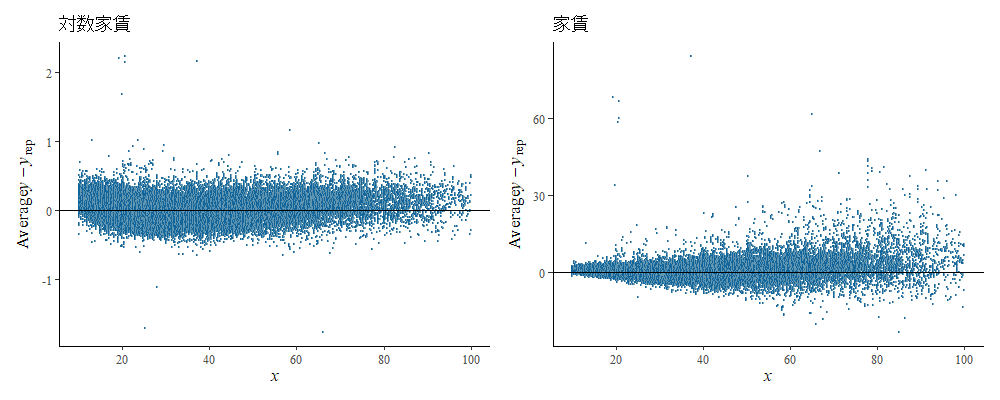
左の図を見ると、y=0の直線の上下にだいたい均等に分布しているので、回帰モデルの前提である残差の等分散性と正規性がだいたい満たされていそうです。おおむね悪くなさそうです。
ただ、x <= 15m2くらいの面積が小さいゾーンで縦軸が正の点が多いことが分かります。つまり15m2を切るような物件では過少に予測しがちということですね。10m2未満の物件を除外しましたが、除外する閾値を15m2に上げてもよかったかもしれません。
また、70m2~以上の物件も同様に過少に予測しがちでした。この面積帯はファミリー向けなので、一人暮らし~二人暮らしゾーンの20~60m2程度の物件とはちょっとメカニズムが違うのかもしれません。
結果
ようやく結果を見るところまでたどり着きました。こちらが推定されたパラメータの結果です。ただしprintが長くなるのでa[s],
b[s]は省略します。
print(fit, pars=c("a0", "b0", "age_b", "walk_b", "sigma_a", "sigma_b", "sigma"), digits_summary=3)
#> Inference for Stan model: anon_model.
#> 4 chains, each with iter=5000; warmup=1000; thin=1;
#> post-warmup draws per chain=4000, total post-warmup draws=16000.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
#> a0 -0.101 0 0.015 -0.131 -0.111 -0.101 -0.091 -0.071 25141 1
#> b0 0.804 0 0.006 0.792 0.800 0.804 0.808 0.817 22027 1
#> age_b -0.011 0 0.000 -0.011 -0.011 -0.011 -0.010 -0.010 17203 1
#> walk_b -0.009 0 0.000 -0.009 -0.009 -0.009 -0.009 -0.009 28102 1
#> sigma_a 0.313 0 0.011 0.292 0.306 0.313 0.321 0.337 20686 1
#> sigma_b 0.137 0 0.005 0.128 0.133 0.136 0.140 0.146 26200 1
#> sigma 0.125 0 0.000 0.125 0.125 0.125 0.125 0.126 15352 1
#>
#> Samples were drawn using NUTS(diag_e) at Sun Dec 24 15:16:08 2023.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).
築年数効果
以下、点推定値としてmedianを採用します4。$\beta_{\mathrm{age}}$ = -0.011でした。これは、築年数が1年増えるごとに、家賃+管理費の対数が0.011小さくなることを意味します。
と言われてもよく分からないですね。また、築年数が$m$年の物件は新築と比べてどの程度家賃が下がるのかも知りたいです。
この疑問に答えるには、$\mathrm{age}_{i} = 1, \dots, 40$としたときの$\exp (\beta_{\mathrm{age}} \mathrm{age}_{i})$の事後中央値と95%ベイズ信用区間を求めればよいです。tidybayes::spread_draws()を使うとrstan::sampling()の返り値からサンプルをtidyな形で取り出すことができて計算が楽です。
Code
tidy_draws <- tidybayes::spread_draws(fit, age_b, walk_b, sigma_a, sigma_b, sigma)
age_b <- tidy_draws |>
pull(age_b)
# 1年 - 40年
res_age <- 1:40 |>
map_dfr(\(age) {
samples <- exp(age_b * age)
tibble::tibble(
age=age,
median=quantile(samples, 0.5),
lower=quantile(samples, 0.975),
upper=quantile(samples, 0.025)
)
})
# きりのいいageだけ表示する
res_age |>
filter(age %in% c(0:5, seq(5, 40, 5))) |>
print(n=15)
#> # A tibble: 12 × 4
#> age median lower upper
#> <int> <dbl> <dbl> <dbl>
#> 1 1 0.990 0.990 0.990
#> 2 2 0.979 0.979 0.979
#> 3 3 0.969 0.969 0.969
#> 4 4 0.959 0.959 0.959
#> 5 5 0.949 0.949 0.949
#> 6 10 0.900 0.901 0.900
#> 7 15 0.854 0.855 0.854
#> 8 20 0.810 0.811 0.810
#> 9 25 0.769 0.770 0.768
#> 10 30 0.730 0.731 0.729
#> 11 35 0.692 0.693 0.691
#> 12 40 0.657 0.658 0.656
medianは事後分布の中央値、upperとlowerは95%CIの上限と下限です。
medianの列の通り、築年数が1年増えるごとに家賃は0.99倍になります。新築の物件と比較すると、築5年の物件で5%、10年で10%、15年で15%、20年で19%家賃が下がります。築25年くらいまではほぼ1年で1%減ると近似できて覚えやすいです5。これは参考にできそうな知見ですね。個人的に参考にしようと思いました。
物件数が18万件と多いおかげでサンプルの標準誤差が小さいためにmedianもupperもlowerもほぼ一致しています。データ数は正義。
次の徒歩分数や最寄り駅別の家賃相場の結果も同様ですが、「築年数が1年増えるごとに家賃は0.99倍」というのは今回設定したモデルでの数値であって、モデルの設定が変われば数値も変わることに注意してください。
最寄り駅からの徒歩分数効果
最寄り駅からの徒歩分数が伸びるとどの程度家賃が下がるのでしょうか?築年数効果と同じように、$\mathrm{walk}_{i} = 2, \dots, 20$としたときの$\exp (\beta_{\mathrm{walk}} (\mathrm{walk}_{i} - 1))$の事後中央値と95%ベイズ信用区間を求めれば分かります。
Code
walk_b <- fit |>
tidybayes::spread_draws(walk_b) |>
pull(walk_b)
# 2分 - 20分
res_walk <- 2:20 |>
map_dfr(\(walk) {
samples <- exp(walk_b * (walk - 1))
tibble::tibble(
walk=walk,
median=quantile(samples, 0.5),
lower=quantile(samples, 0.975),
upper=quantile(samples, 0.025)
)
})
# きりのいいwalkだけ表示する
res_walk |>
filter(walk %in% c(2, 3, 5, 10, 15, 20)) |>
print()
#> # A tibble: 6 × 4
#> walk median lower upper
#> <int> <dbl> <dbl> <dbl>
#> 1 2 0.991 0.991 0.991
#> 2 3 0.982 0.982 0.982
#> 3 5 0.964 0.965 0.964
#> 4 10 0.921 0.923 0.920
#> 5 15 0.880 0.882 0.878
#> 6 20 0.841 0.844 0.838
駅からの徒歩分数が1分増えるごとに家賃は0.991倍になります。駅から徒歩1分の物件と比較すると、家賃は徒歩5分の物件で4%、10分で8%、15分で12%、20分で16%下がるようです。
ただし、新築と築数年や、徒歩1分と徒歩5分などはもう少しだけ離れていても不思議ではないかなという気もします。
最寄り駅別の家賃相場(面積固定)
最寄り駅によってどの程度家賃が変わるか見てみましょう。同一の路線内で見るとイメージが付いて面白いです。
実際のところ、新築で徒歩1分の物件はあまりないので相場感をイメージしづらいですね。現実的なところで築5年、徒歩5分で30m2の物件の相場を見てみましょう。これは$\mathrm{area}_{i} = 30, \mathrm{age}_{i} = 5, \mathrm{walk}_{i} = 5$としたときの$\exp(\mu_{i})$の事後中央値と95%ベイズ信用区間を計算します。
京王線・京王新線です。新宿から西の方に伸びる路線ですね。北の方にJR中央線、南の方に小田急線が並行して走っています。
Code
# 駅名とモデルに投入したindexのマッピング
sta_chr_idx_table <- df_mod |>
select(moyorieki_1_station, moyorieki_1_station_index) |>
distinct(moyorieki_1_station, .keep_all=TRUE)
# 駅名があればそのindex, なければNA_integer_を返す
station_to_idx <- function(station_name) {
chr <- sta_chr_idx_table$moyorieki_1_station
idx <- sta_chr_idx_table$moyorieki_1_station_index
if (length(idx[which(chr==station_name)]) == 0) {
return(NA_integer_)
} else {
return(idx[which(chr==station_name)])
}
}
tidy_draws_by_idx <- tidybayes::spread_draws(fit, a[idx], b[idx], age_b, walk_b, sigma_a, sigma_b)
stations <- c(
"新宿駅", "初台駅", "幡ヶ谷駅", "笹塚駅", "代田橋駅", "明大前駅", "下高井戸駅", "桜上水駅", "上北沢駅", "八幡山駅", "芦花公園駅", "千歳烏山駅"
)
# factor型で駅の路線順に並べる
stations_fct <- forcats::fct_relevel(as.factor(stations), stations)
# 見る駅名のindex(stanのa[s]やb[s]のs)
idxs <- map_int(stations, station_to_idx)
area <- 30
age <- 5
walk <- 5
p1 <- tidy_draws_by_idx |>
filter(idx %in% idxs) |>
# 駅のindexではなく駅名をプロットに付けるためにindexと駅名のテーブルをjoinする
left_join(
df_mod |>
filter(moyorieki_1_station %in% stations) |>
distinct(moyorieki_1_station, .keep_all=TRUE) |>
select(moyorieki_1_station, moyorieki_1_station_index) |>
rename(station=moyorieki_1_station, idx=moyorieki_1_station_index) |>
mutate(station=forcats::fct_relevel(station, stations)),
by="idx"
) |>
mutate(mu_exp=exp(a+b*log(area)+age_b*age+walk_b*(walk-1))) |>
ggplot(aes(mu_exp, station))+
theme_light()+
tidybayes::stat_pointinterval(point_interval=tidybayes::median_qi, .width=0.95)+
scale_x_continuous(breaks=0:20)+
theme(axis.title.y=element_blank())+
labs(
title="exp(mu_i) (age_i=5, walk_i=5, area_i=30)",
subtitle="point: estimated (median), bar: 95% bayesian CI",
x="exp(mu_i)",
y="station"
)
p2 <- df_mod |>
filter(moyorieki_1_station %in% stations) |>
count(moyorieki_1_station, moyorieki_1_station_index, name="n") |>
rename(station=moyorieki_1_station, idx=moyorieki_1_station_index) |>
mutate(station=forcats::fct_relevel(station, stations)) |>
arrange(station) |>
ggplot(aes(station, n))+
theme_light()+
geom_bar(stat="identity", color="black", fill="gray", alpha=0.6)+
scale_y_continuous(breaks=seq(0, 2000, 500), minor_breaks=seq(0, 2000, 100))+
geom_text(aes(label=n, y=100))+
theme(axis.title.y=element_blank())+
coord_flip()+
labs(
title="(参考)物件数",
subtitle="築40年以下, 徒歩20分以下, 10m2-100m2の物件のみ"
)
patchwork::wrap_plots(p1, p2, ncol=2, widths=c(3, 2))
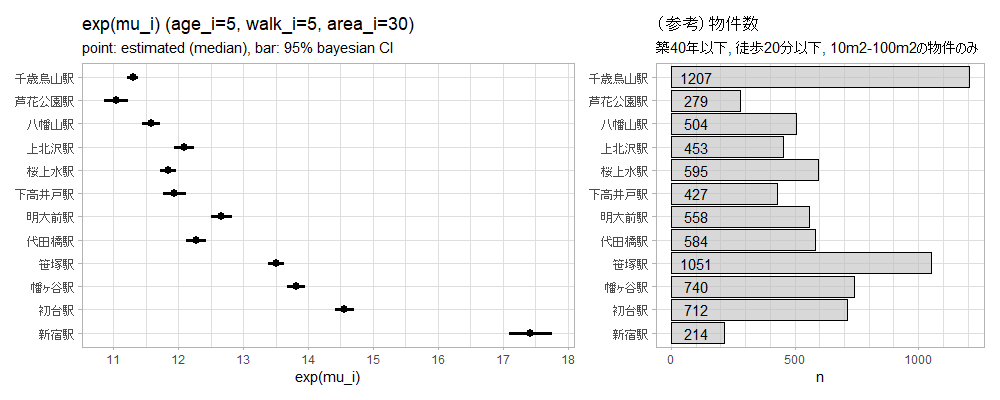
y軸は路線図の順番通りに駅を並べています。物件数も合わせて示しているのは、そもそもそのエリアに物件がどのくらいあるのかという参考です。なお、家賃相場のモデルには路線名を入れていないので、左のプロットの推定家賃相場は京王線の新宿もJRなどの他の路線の新宿も同じになります。また、最寄り駅が新宿駅という物件数には、京王線以外の新宿駅が最寄り駅の物件も含まれています。
左の図の点は事後中央値、点の左右の棒は95%ベイズ信用区間です。今回設定したモデルの下では、新宿から徒歩5分、築5年の30m2の物件の相場は17.4万円(95%CI: 17.1万円-17.8万円)ということです。
今回設定したモデルの下では「新宿から徒歩5分の築5年の30m2の物件の家賃の平均的な姿」というパラメータがあり、これに「新宿から徒歩5分の築5年の30m2の物件の家賃相場」と名付けるなら、「家賃相場」の確率分布の95%は17.1万円-17.8万円の間に入るということを意味します。繰り返しですがモデル式が変われば図で示した家賃相場の数値は当然変わります。新宿から徒歩5分、築5年、30m2の実際の物件を集めて中央値を取ったら17.4万円でしたということでもありません。
また、実際に観測される物件の家賃は、家賃相場にさらに$\sigma$というノイズが乗ります6。モデルに入れていない特徴量による物件の特徴での加算・減算分や、その他の説明のつかなかった色々なものを示します。なので、新宿から徒歩5分の築5年の30m2の物件の実際の家賃は、その95%が17.1万円-17.8万円の間に入るということではなく、17.1万円より小さいものから17.8万円より大きいものまでもっとあります。信用区間と予測区間の違いですね。
この図に限らず知っている駅や路線をいくつか見てみると、だいたいの金額や駅間の相対的な水準はそんなに外してはいないかなと思いました。
図に戻りますが、直感通り、新宿から遠ざかるほど相場が下がっていきます。明大前と代田橋は明大前の方が新宿から遠いですが、明大前の方が少し高いのは特急~各駅の全ての列車が止まること、井の頭線も通っているので渋谷や吉祥寺に出やすいからでしょうか。同様に千歳烏山は芦花公園より高いですが、千歳烏山も全ての列車が止まることが理由でしょうか。ただし95%ベイズ信用区間が広くて被っているので明確に差があるとは言いづらいです。
千歳烏山の次の駅は仙川です。千歳烏山と仙川の間の東側が世田谷区、西側が調布市です。23区の物件をスクレイピングした都合上、最寄り駅が仙川という物件のうち、世田谷区にある物件しかデータに存在しません。これが仙川の推定値にどの程度影響を与えるか分からないので、仙川の相場は表には載せませんでした。
わたし的には幡ヶ谷~桜上水がよさそうで気になりました。13.5万円前後の幡ヶ谷と笹塚は新宿まで5分、12.5万円の明大前は新宿と渋谷に10分で出られます。12万円弱の桜上水は駅の数としては新宿から離れますが急行が止まるので新宿まで15分です。閑静な住宅街という街ですね。安いかと言われるとどこも安くはないですが、新宿へのアクセスの良さを考えるとなかなかいいような気がします。
ちなみに上の図はpatchworkというggplot2オブジェクトを上下左右に並べられるパッケージを使っています。このように左のプロットと右のプロットを3:2の幅で並べるという並べ方も簡単にできます。重宝するパッケージです。
京王線・京王新線は新宿から遠ざかるほど家賃が安くなり、速達列車が止まる駅はすこしお高くなりました。都心と郊外を結ぶ路線はおおむねこのパターンです。一方で、都内の2駅を結ぶ路線はちょっと変わります。
次の図は東急池上線(五反田~蒲田)です。池上線は各駅停車のみの路線です。
Code
stations <- c(
"五反田駅", "大崎広小路駅", "戸越銀座駅", "荏原中延駅", "旗の台駅", "長原駅", "洗足池駅", "石川台駅", "雪が谷大塚駅", "御嶽山駅", "久が原駅", "千鳥町駅", "池上駅", "蓮沼駅", "蒲田駅"
)
stations_fct <- forcats::fct_relevel(as.factor(stations), stations)
idxs <- map_int(stations, station_to_idx)
area <- 30
age <- 5
walk <- 5
p1 <- tidy_draws_by_idx |>
filter(idx %in% idxs) |>
left_join(
df_mod |>
filter(moyorieki_1_station %in% stations) |>
distinct(moyorieki_1_station, .keep_all=TRUE) |>
select(moyorieki_1_station, moyorieki_1_station_index) |>
rename(station=moyorieki_1_station, idx=moyorieki_1_station_index) |>
mutate(station=forcats::fct_relevel(station, stations)),
by="idx"
) |>
mutate(mu_exp=exp(a+b*log(area)+age_b*age+walk_b*(walk-1))) |>
ggplot(aes(mu_exp, station))+
theme_light()+
tidybayes::stat_pointinterval(point_interval=tidybayes::median_qi, .width=c(0.95))+
scale_x_continuous(breaks=0:20)+
theme(axis.title.y=element_blank())+
labs(
title="exp(mu_i) (age_i=5, walk_i=5, area_i=30)",
subtitle="point: estimated (median), bar: 95% bayesian CI",
x="exp(mu_i)",
y="station"
)
p2 <- df_mod |>
filter(moyorieki_1_station %in% stations) |>
count(moyorieki_1_station, moyorieki_1_station_index, name="n") |>
rename(station=moyorieki_1_station, idx=moyorieki_1_station_index) |>
mutate(station=forcats::fct_relevel(station, stations)) |>
arrange(station) |>
ggplot(aes(station, n))+
theme_light()+
geom_bar(stat="identity", color="black", fill="gray", alpha=0.6)+
scale_y_continuous(breaks=seq(0, 2000, 500), minor_breaks=seq(0, 2000, 100))+
geom_text(aes(label=n, y=100))+
theme(axis.title.y=element_blank())+
coord_flip()+
labs(
title="(参考)物件数",
subtitle="築40年以下, 徒歩20分以下, 10m2-100m2の物件のみ"
)
patchwork::wrap_plots(p1, p2, ncol=2, widths=c(3, 2))
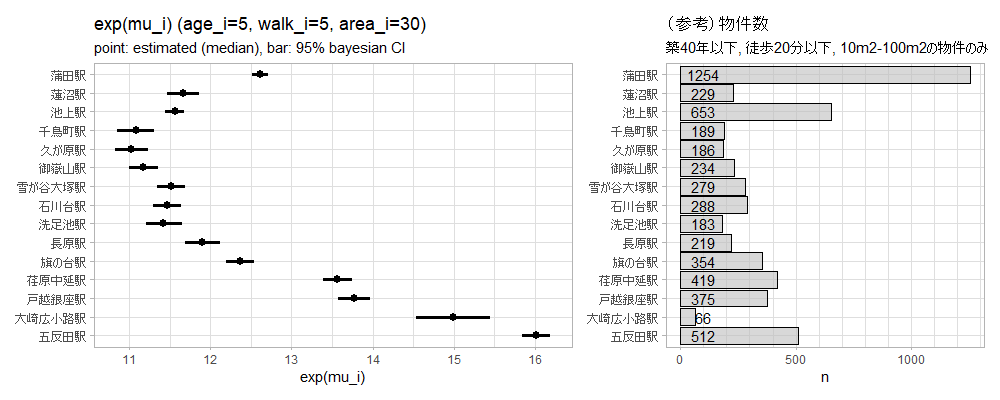
五反田と蒲田が高く、その間が比較的安くなります。アルファベットの大文字のJの文字を時計回りに90度回転させたような図になります。京王井の頭線(渋谷~吉祥寺)もこのパターンです。
大崎広小路は物件数が66件しかないですが、階層モデルのおかげでパラメータが推定できています(当然、95%ベイズ信用区間は広くなります)。
東京メトロや都営地下鉄のように都心を横切るような路線だと真ん中あたりが高くなることもあります。
階層モデルによって面積や築年数や徒歩分数要素を分離して同じ条件で比較できるようになったことで、条件を固定したときの最寄り駅による家賃の違いを知ることができました。Stan(MCMC)のおかげでパラメータの確率分布が得られるので、だいたい17.1万円-17.8万円の間という幅も分かっていいですね。家賃相場は17.4万円ですと言われても、だいたい17.1万円-17.8万円なのかだいたい15万円-20万円なのかでは話が変わってきますからね。
最寄り駅別の家賃相場(面積可変)
築5年、徒歩5分は固定のまま、面積を20m2から60m2まで変えたときに最寄り駅によってどの程度家賃相場が変わるのか見てみましょう。$\mathrm{age}_{i} = 5, \mathrm{walk}_{i} = 5$としたときの、$\mathrm{area}_{i}$を20から60まで変えたときの$\exp(\mu_{i})$の事後中央値と95%ベイズ信用区間を計算します。
Code
stations <- c("初台駅", "幡ヶ谷駅", "笹塚駅")
stations_fct <- forcats::fct_relevel(as.factor(stations), stations)
idxs <- map_int(stations, station_to_idx)
# MCMCの取り出したサンプルが必要(上で一度実行しているのでコメントアウトで再掲)
# sample_a <- rstan::extract(fit, "a")$a
# sample_b <- rstan::extract(fit, "b")$b
# sample_age_b <- rstan::extract(fit, "age_b")$age_b
# sample_walk_b <- rstan::extract(fit, "walk_b")$walk_b
# sample_sigma_a <- rstan::extract(fit, "sigma_a")$sigma_a
# sample_sigma_b <- rstan::extract(fit, "sigma_b")$sigma_b
# sample_sigma <- rstan::extract(fit, "sigma")$sigma
area_rent_table <- tidyr::expand_grid(
idx=idxs,
area=20:60,
age=5,
walk=5
) |>
left_join(
df_mod |>
filter(moyorieki_1_station %in% stations) |>
distinct(moyorieki_1_station, .keep_all=TRUE) |>
select(moyorieki_1_station, moyorieki_1_station_index) |>
rename(station=moyorieki_1_station, idx=moyorieki_1_station_index) |>
mutate(station=forcats::fct_relevel(station, stations)),
by="idx"
) |>
mutate(
mu=pmap(list(idx=idx, area=area, age=age, walk=walk), \(idx, area, age, walk) {
sample_a[,idx] + sample_b[,idx]*log(area) + sample_age_b*age + sample_walk_b*(walk - 1)
})
) |>
mutate(
mu_exp_median=exp(map_dbl(mu, \(x) quantile(x, 0.5))),
mu_exp_lower=exp(map_dbl(mu, \(x) quantile(x, 0.025))),
mu_exp_upper=exp(map_dbl(mu, \(x) quantile(x, 0.975)))
)
area_rent_table |>
ggplot(aes(area, color=station, fill=station))+
theme_light()+
geom_ribbon(aes(ymin=mu_exp_lower, ymax=mu_exp_upper), alpha=0.2)+
geom_line(aes(y=mu_exp_median))+
scale_y_continuous(breaks=seq(5, 30, 5), minor_breaks=5:30)+
ggsci::scale_color_aaas()+
ggsci::scale_fill_aaas()+
theme(legend.title=element_blank())+
labs(
title="exp(mu_i) (age_i=5, walk_i=5, area_i=20 - 60)",
subtitle="center line: estimated (median), ribbon: 95% bayesian CI",
x="area(面積)",
y="exp(mu_i)",
)
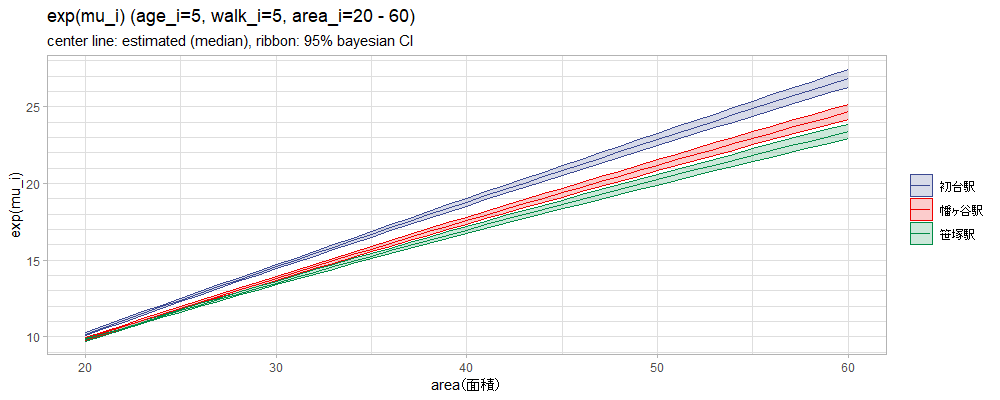
三色のバンドの中にある線は事後中央値、その上下の線は95%ベイズ信用区間です。
初台、幡ヶ谷、笹塚の3駅を見ると、20m2~30m2のゾーンでは家賃はあまり変わりませんが、面積が大きくなると初台>幡ヶ谷>笹塚の順に家賃が変わってきます。
これは結局、面積の増加に対する対数家賃の増え方のパラメータであるbが、初台>幡ヶ谷>笹塚の順に大きいからですね。以下の表は、$b_{sta[i]}$の事後中央値(表のb)、95%ベイズ信用区間(.lower,
.upper)です。
Code
# print(fit, pars=c("b[89]", "b[173]", "b[353]"))
tidy_draws_by_idx |>
filter(idx %in% idxs) |>
left_join(
df_mod |>
filter(moyorieki_1_station %in% stations) |>
distinct(moyorieki_1_station, .keep_all=TRUE) |>
select(moyorieki_1_station, moyorieki_1_station_index) |>
rename(station=moyorieki_1_station, idx=moyorieki_1_station_index) |>
mutate(station=forcats::fct_relevel(station, stations)),
by="idx"
) |>
ungroup() |>
group_by(station) |>
tidybayes::median_qi(b, .width=0.95) |>
select(station, b, .lower, .upper)
#> # A tibble: 3 × 4
#> station b .lower .upper
#> <fct> <dbl> <dbl> <dbl>
#> 1 初台駅 0.883 0.858 0.907
#> 2 幡ヶ谷駅 0.836 0.814 0.859
#> 3 笹塚駅 0.791 0.770 0.812
なので、面積が大きくなるほど家賃相場が開いていきます。
R|階層線形モデルで渋谷区の賃貸価格を予想する|hanaoriの記事にインスピレーションをいただいた内容です。
おわりに
任意の築年数、徒歩分数、面積、最寄り駅のもとでの家賃相場を推定できました。Stanではドメイン知識を活かして考えたモデルをそのままコードに落として推定や解釈ができるので楽しいですね。住みたい駅を見つけるのに使えそうです。
わたし自身が知りたかった内容を知ることができたのでよかったです。個人開発は自分が使いたいものを作ろうという話がありますが、まさにその通りでした。
今回のモデルでは、築年数と徒歩分数が対数家賃を押し下げる効果は線形でかつ一律としました。しかし、新築や徒歩1~2分のような物件は、築数年や徒歩5分程度の物件と比べてさらに高い可能性もあります。新築のプレミアムのようなイメージですね。
また、減価効果は駅によっても違うかもしれません。特に都心の真ん中の新築物件や駅近物件は、他の駅の新築物件や駅近物件よりもプレミアムが乗る可能性があります。一方で、同じ駅近でも地下鉄ではなく地上を走る路線沿いや大きな駅の近くの場合は、騒音などの影響でプレミアムが乗らない可能性もあります。
築年数による減価効果は建物の材質や駅からの徒歩距離によっても変わりそうです。木造より鉄筋の方が、また駅から遠い物件より駅近物件の方が、築年数が経過しても価値が下がりにくいかもしれません。
しかし、全体の傾向をつかむという目的のモデルでは、一律でもそこまで悪くないだろうということで定式化しました(今回は建物の材質のデータは取れていないこともあります)。
他にも特徴量を追加することでさらに説明力のあるモデルが作れそうです。Future Work、今後の課題ということで以下に示します。
- 最寄り駅を複数考慮
- 今回は最大で3つある最寄り駅のうち1番上に書いてあるものしか使っていない
- 同じ幡ヶ谷が最寄り駅でも、初台寄りの幡ヶ谷と笹塚寄りの幡ヶ谷だと平均的には前者の方がすこし高そう。最寄り駅の情報を複数使うと、最寄り駅効果をよりよく推定できそう
- 地図は二次元平面なので二次元の位置関係を考慮するということ
- 物件の階数や建物の高さ
- 1階は安く最上階は高い
- 物件の階数が上がるほど高い
- 階数が高い建物はその分設備が豪華になる傾向にありそうなので家賃も上がりそう
- 物件の構造や設備の有無
- 鉄筋なら高そうだし、バストイレ別とか角部屋だとやはり高そう
- 鉄筋か木造かのような物件の構造は築年数による減価効果に影響がありそう
- 近所の店舗情報と駅の位置関係
- スーパーマーケットが近所100mか500mかで違いそうだし、同じ100mでも、駅 - スーパー - 物件という位置関係の方が、駅 - 物件 - スーパーという位置関係よりも家賃が高そう(駅からの帰りに寄れる)
参考にした記事など
先行研究
- データ解析で割安賃貸物件を探せ!(山手線沿線編) - StatModeling Memorandum
- R|階層線形モデルで渋谷区の賃貸価格を予想する|hanaori
- 回帰分析と機械学習で中央線の高コスパ物件を探す(スクレイピング+前処理) - sola
- 機械学習を使って東京23区のお買い得賃貸物件を探してみた - データで見る世界
- 【ForecastFlow×LLoco】機械学習を使って会社近くのお得物件をSUUMOから探し出せ 〜(1)問題設定・データ取得編〜|CO-WRITE
- Pythonによる不動産情報のデータ取得&分析(1)【賃貸物件/Webスクレイピング編】 - akatak blog
- 【Pythonで不動産データ分析!】機械学習(ランダムフォレスト)を用いてSUUMOからお得物件を探してみた!
bayesplotのプロット
- Bayesplotパッケージはいいよ – Kosugitti’s BLOG
- Introduction to bayesplot (mcmc_ series)
- Introduction to bayesplot (ppc_ series) - nora_goes_far
- [R] [stan] bayesplot を使ったモンテカルロ法の実践ガイド - ill-identified diary
書籍
単純に平均するのは、「その街の家賃相場」は実際にある物件の築年数を含めたものとして算出するという考えによるので、どちらが正しいということではありません。 ↩︎
家賃10万円で敷金1ヶ月礼金1ヶ月(=2年で260万円)の物件と、家賃10.5万円で敷金礼金なし(=2年で252万円)の物件なら、他の全ての条件が同じなら後者を選びそうですが、分かりやすくするため ↩︎
SUUMOの利用規約を読んだところ、スクレイピングを特に禁じてはいないと理解しています。 ↩︎
この後expをかけて対数を外したパラメータを示しますが、medianは変数変換に依存しないからです。 ↩︎
テイラー展開より、$x=0$のまわりなら$(1-x)^n \approx -nx$なので$-nx$で近似できるということです。 ↩︎
正確には、$N(\mu_{i}, \sigma)$から生成される$\log{y_{i}}$のexpを取ったもの ↩︎