カルマンフィルタで株式のベータ値を推定する
概要
- 個別株式のリスクが市場全体のリスクと比べてどの程度大きいかを示す「ベータ値」という数値があります。
- 精緻化された「時変ベータ」を求めるため、ベータ値の変動を状態空間モデルで定式化し、カルマンフィルタを用いて東京電力のベータ値を推定してみました。
- カルマンフィルタはPythonでフルスクラッチで書きました。なお、参考までにRのKFASを使ったバージョンも付けています。
- 経済・ファイナンスのためのカルマンフィルター入門(森平,
2019)でも述べられているように、東京電力株は株価の値動きが景気変動に影響を受けづらいディフェンシブ銘柄の代表格とされてきましたが、ベータ値は2011年の東日本大震災や原発事故の時期を境に急上昇したことが分かりました。
- この書籍で用いている状態空間モデルと本記事で用いた状態空間モデルは若干違います(後述)。
- Pythonでのカルマンフィルタの実装は「カルマンフィルタの実装」の章をご覧ください。結果を見たい方は「ベータ値(カルマンフィルタ版)」の章をご覧ください。
ベータ値とは
TOPIXなどの市場全体の株価と比べて、個別株式などの株価がどの程度大きく動く傾向かというリスクの指標です。個別株式のリスクの大きさを示す指標としてよく使用されます。なお、金融リスクの分野でいうリスクとは、一般的に値動きの激しさを示します。リターンの分布の分散のイメージです。
例えば、対日経平均株価のベータ値が1.5の銘柄は、日経平均が1%動くと平均的に1.5%動くことを示します。1より大きい銘柄は、値上がるときは市場平均よりも大きく上がるものの、値下がるときは市場平均よりも大きく下がる傾向にあります。一方、1より小さい銘柄は、値上がるときは市場平均よりも上がらないものの、値下がるときは市場平均よりも小幅な下げにとどまりやすいです。
ベータ値は一般的には0~2程度を取ることが多いです。負の値を取ることもあり得ます。景気に敏感なセクターである電気機器セクターや機械セクターの銘柄は1より大きく、景気に左右されにくい電気・ガスセクターや食品セクターといった内需型のセクターは1より小さい傾向にあります。各銘柄のベータ値は例えば日経電子版のベータ値高位ランキングなどで見ることができます。
ベータ値は、個別株式のポジションのヘッジポジションを組むためにも使われます。個別株式のリスクは、市場全体に由来するリスクと個別株式に由来するリスクに分解されます。個別株式の買いポジションを持っているとき、その買いポジションの金額にベータ値を掛けた金額だけ株価指数の売りポジションを持つと、市場全体から来る変動を打ち消すことができます1。
ベータ値の定式化
$S_{t}, S_{t}^{M}$をそれぞれ、$t (1, \dots, T)$日における個別株式とマーケット指数の終値とします。「マーケット指数」は、日経平均株価やTOPIXなどです。
$t$日における個別株式とマーケット指数の対前日リターンをそれぞれ$r_{t}, r_{t}^{M}$とすると、対数リターンは以下で計算できます2。
$$ \begin{align*} r_{t} &= \log S_{t} - \log S_{t-1} \\\ r_{t}^{M} &= \log S_{t}^{M} - \log S_{t-1}^{M} \end{align*} $$
このとき、$t$日におけるベータ値は、以下の$\beta_{t}$です。
$$ r_{t} = \alpha_{t} + \beta_{t} r_{t}^{M} + \epsilon_t, \quad \epsilon_{t} \sim N(0, \sigma^2) $$
$\beta_{t}$は、過去一定期間の$r_{t}, r_{t}^{M}$を用いて回帰で求められます。過去1年~3年=250営業日~750営業日とすることが多いように思います。この期間を1日ずつずらしてローリング回帰することで各$t$における$\beta_{t}$を得るというのが簡単な推定方法です。
しかしこの方法は簡略化しているため、いくつか問題点があります。ローリング回帰に用いた標本期間$t-i+1, \dots, t$日の間はベータ値は一定と仮定していますが、実際にはそうではありません。ある日にベータ値が急に動いたとしても、この方法では変動は遅れてマイルドにしか現れません。また$i$をいくつに設定するかによってベータ値が変わります。
状態空間モデルを用いてベータ値を動的に定式化することで、これらの問題を解消することができます。この記事では、最もオーソドックスだと思われる以下の状態空間モデルを推定します3。
$$ \begin{align*} r_{t} &= \alpha_{t} + \beta_{t} r_{t}^{M} + e_{t}, &e_t \sim N(0, \sigma_{e}^2) \\\ \alpha_{t} &= \alpha_{t-1} + \epsilon_{t}, &\eta_t \sim N(0, \sigma_{\epsilon}^2) \\\ \beta_{t} &= \beta_{t-1} + \eta_{t}, &\eta_t \sim N(0, \sigma_{\eta}^2) \end{align*} $$
$\beta_{t}$がベータ値です。これは時変ベータと呼ばれます。1本目の式が観測方程式、2本目と3本目の式が状態方程式の状態空間モデルで、ベータ値が日々確率的に変動することを示しています。
最初のベーシックな方法でのベータ値は、このモデルの2本目と3本目の式をなくしたものですね。時系列回帰が静的から動的になったと考えてもいいです(動的な時系列回帰をするために回帰タイプの状態空間モデルを組むというのはよくあるパターンです)。
このような、線形で誤差項が正規分布の状態空間モデルでは、状態空間モデルの状態(上のモデルでは$\alpha_{t}, \beta_{t}$)の平均と分散・共分散は、カルマンフィルタというアルゴリズムによって解析的に行列計算で高速に求められます。
この記事では、まずベータ値とは何かをイメージするために最初の方法でのベータ値を示します。次に後者の時変ベータをカルマンフィルタで実装することで時変ベータをみてみます。
環境
株価の取得はpandas-datareader, DataFrameのハンドリングはpolars, プロットはplotnineを使います。
カルマンフィルタはnumpyとscipyで自分で一から実装しました。最初はpykalmanといういい感じのライブラリを見つけたのですが、メンテが止まっており、GitHubのissueに立っているエラーと同じエラーが出て動きませんでした。
- Windows 10
- Python 3.11.5
- numpy 1.26.0
- pandas-datareader 0.10.0
- polars 0.19.6
- plotnine 0.12.3
- patchworklib 0.6.2
- scipy 1.11.3
import numpy as np
import scipy as sp
import pandas_datareader.data as pdr
import polars as pl
import patchworklib as pw
from plotnine import *
株価データの取得
2001/1/5~2023/12/29の東京電力と日経平均株価を取得しました。
株価はpandas_datareader.data.DataReaderを用いてStooqから取得します。一定期間の個別株式と日経平均の終値が取得できればデータソースは何でも構いません。
東京電力と日経平均の終値からそれぞれ対前日の対数リターンを計算しておきます。対数リターンは%表記できるように100倍します。また、最初の日のリターンは計算できないので最初の日のレコードを除きます。
STOCK_CODE = "9501.JP"
MARKET_CODE = "^NKX"
START_DATE = "2001-01-01"
END_DATE = "2023-12-29"
stock = pdr.DataReader(STOCK_CODE, data_source="stooq", start=START_DATE, end=END_DATE)
# pd.reset_index()でindexにあるdateをカラムとして持つ
df_stock = pl.from_pandas(stock.reset_index())
df_stock = (
df_stock
.sort("Date")
# 数レコードだけ株価がnullの日付があるが、nullの場合は削除する
.filter(pl.col("Close").is_not_null())
.with_columns(
Date=pl.col("Date").dt.date(),
ret=(pl.col("Close").log() - pl.col("Close").shift(1).log())*100
)
.slice(1)
)
market = pdr.DataReader(MARKET_CODE, data_source="stooq", start=START_DATE, end=END_DATE)
df_market = pl.from_pandas(market.reset_index())
df_market = (
df_market
.sort("Date")
.filter(pl.col("Close").is_not_null())
.with_columns(
Date=pl.col("Date").dt.date(),
ret=(pl.col("Close").log() - pl.col("Close").shift(1).log())*100
)
.slice(1)
)
df = (
df_stock
.rename({"Date": "date", "Close": "close_stock", "ret": "ret_stock"})
.select("date", "close_stock", "ret_stock")
.join(
df_market
.rename({"Date": "date", "Close": "close_market", "ret": "ret_market"})
.select("date", "close_market", "ret_market"),
how="inner",
on="date"
)
)
こんな感じのDataFrameです。closeは終値、retはリターン(%)、_stockは東京電力、_marketは日経平均を指します。
polarsはDataFrameをprintしたときに各カラムのデータ型を書いてくれるのも素敵ですね。
print(df)
shape: (5_632, 5)
┌────────────┬─────────────┬───────────┬──────────────┬────────────┐
│ date ┆ close_stock ┆ ret_stock ┆ close_market ┆ ret_market │
│ --- ┆ --- ┆ --- ┆ --- ┆ --- │
│ date ┆ f64 ┆ f64 ┆ f64 ┆ f64 │
╞════════════╪═════════════╪═══════════╪══════════════╪════════════╡
│ 2001-01-05 ┆ 2800.0 ┆ -2.469261 ┆ 13867.61 ┆ 1.278143 │
│ 2001-01-09 ┆ 2805.0 ┆ 0.178412 ┆ 13610.51 ┆ -1.871362 │
│ 2001-01-10 ┆ 2840.0 ┆ 1.240051 ┆ 13432.65 ┆ -1.315398 │
│ 2001-01-11 ┆ 2850.0 ┆ 0.351494 ┆ 13201.07 ┆ -1.739042 │
│ … ┆ … ┆ … ┆ … ┆ … │
│ 2023-12-26 ┆ 733.1 ┆ 0.684372 ┆ 33305.85 ┆ 0.155709 │
│ 2023-12-27 ┆ 735.0 ┆ 0.258838 ┆ 33681.24 ┆ 1.120795 │
│ 2023-12-28 ┆ 736.7 ┆ 0.231025 ┆ 33539.62 ┆ -0.421358 │
│ 2023-12-29 ┆ 738.5 ┆ 0.244035 ┆ 33464.17 ┆ -0.225211 │
└────────────┴─────────────┴───────────┴──────────────┴────────────┘
ベータ値(ベーシック版)
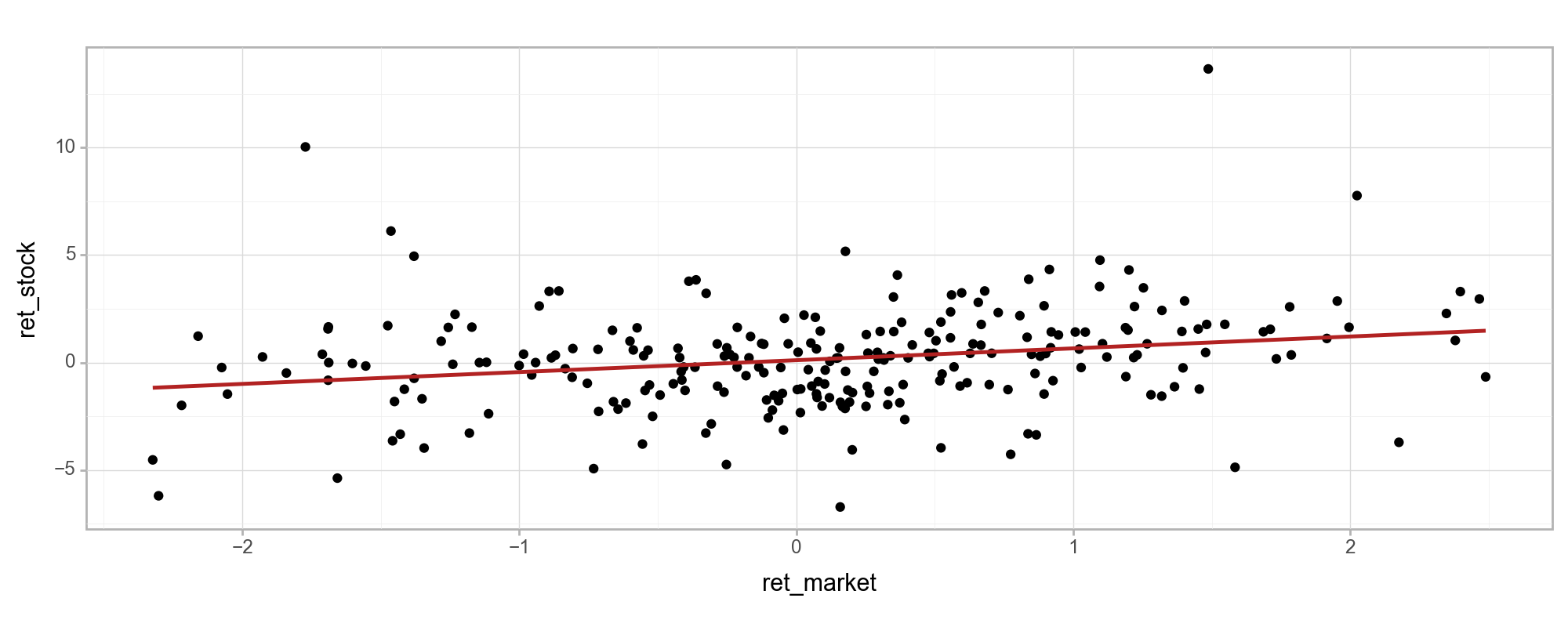
ベーシックな方法でのベータ値は、一定期間の市場全体のリターンを横軸に、個別株式のリターンを縦軸に取って散布図を描き、そこに回帰直線を引いたときの回帰直線の傾きになります。
以下のプロットは、2023/12/29から直近250営業日のリターンの散布図です。赤い線は回帰直線です。赤い線の傾きが、直近250日のデータから計算する2023/12/29のベータ値になります。1を少し下回るくらいです。
Code
(
ggplot(
df.tail(250),
aes("ret_market", "ret_stock")
)
+geom_point()
+theme_light()
+stat_smooth(method="lm", formula="y ~ x + 1", se=False, color="firebrick")
+labs()
+theme(figure_size=(10, 4), dpi=100)
).draw()
以上の方法で各日ごとにローリング回帰すればベータ値を得ることができます。
カルマンフィルタのアルゴリズム
線形・ガウスの状態空間モデルでは、観測誤差 (今回のモデルでは$\sigma_{e}$)と状態誤差($\sigma_{\epsilon}, \sigma_{\eta}$)をパラメータとして与えると、各$t (1, \dots, T)$における状態(今回のモデルでは$\alpha_{t}, \beta_{t}$)の平均と共分散行列は行列計算で解析的に得られます。このアルゴリズムをカルマンフィルタといいます。
ここで得られる状態は以下の2通りです。
- フィルタ化推定量: 各$t$における状態を、$1, \dots, t$の観測値から推定する
- 平滑化推定量: 各$t$における状態を、$1, \dots, T$の観測値から推定する
後者は全時点のデータから状態をbackwardに推定するため、状態の変化は滑らかに、状態の分散は小さく(信頼区間の幅がフィルタ化推定量より狭く)なります。
以下にカルマンフィルタのアルゴリズムを示します。
いま、観測値を$y_{t}$, 状態を$\boldsymbol{x_{t}}$とします。以下、太字の変数は行列、そうではない変数はスカラーを示します。
行列表現で表すと以下の1本目の式が状態方程式、2本目の式が観測方程式です。
$$ \begin{align*} \boldsymbol{x_{t}} &= \boldsymbol{G_{t}} \boldsymbol{x_{t-1}} + \boldsymbol{w_{t}}, &\boldsymbol{w_{t}} \sim N(\boldsymbol{0}, \boldsymbol{W_{t}}) \\\ y_{t} &= \boldsymbol{F_{t}} \boldsymbol{x_{t}} + v_{t}, &v_{t} \sim N(0, V_{t}) \end{align*} $$
ただし、$\boldsymbol{G_{t}}$は状態遷移行列(p x p)、$\boldsymbol{F_{t}}$は観測行列(1 x p)、$\boldsymbol{W_{t}}$は状態誤差の共分散行列(p x p)、$V_{t}$は観測誤差の分散です。
また、状態の事前分布$\boldsymbol{x_{0}}$は$\boldsymbol{x_{0}}\sim N(\boldsymbol{m_{0}}, \boldsymbol{C_{0}})$であり、$\boldsymbol{m_{0}}$はp次元のベクトル、$\boldsymbol{C_{0}}$はp x pの行列です。
フィルタリング
$t-1$での状態のフィルタリング分布の平均と共分散行列$\boldsymbol{m_{t-1}}, \boldsymbol{C_{t-1}}$(それぞれp次元ベクトル、p x pの行列)が与えられると、
- フィルタリング分布: $N(\boldsymbol{m_{t}}, \boldsymbol{C_{t}})$
- $\boldsymbol{m_{t}}, \boldsymbol{C_{t}}$はそれぞれp次元ベクトル、p x pの行列
- 一期先予測分布: $N(\boldsymbol{a_{t-1}}, \boldsymbol{R_{t-1}})$
- $\boldsymbol{a_{t}}, \boldsymbol{R_{t}}$はそれぞれp次元ベクトル、p x pの行列
- 一期先予測尤度: $N(f_{t}, Q_{t})$
- $f_{t}, Q_{t}$はスカラー
は以下で計算できます。
$$ \begin{align*} \boldsymbol{a_{t}} &= \boldsymbol{G_{t}} \boldsymbol{m_{t-1}} \\\ \boldsymbol{R_{t}} &= \boldsymbol{G_{t}} \boldsymbol{C_{t-1}} \boldsymbol{G_{t}}^{\mathrm{T}} + \boldsymbol{W_{t}} \\\ f_{t} &= \boldsymbol{F_{t}} \boldsymbol{a_{t}} \\\ Q_{t} &= \boldsymbol{F_{t}} \boldsymbol{R_{t}} \boldsymbol{F_{t}}^{\mathrm{T}} + V_{t} \\\ \boldsymbol{K_{t}} &= \boldsymbol{R_{t}} \boldsymbol{F_{t}}^{\mathrm{T}} Q_{t}^{-1} \\\ \boldsymbol{m_{t}} &= \boldsymbol{a_{t}} + \boldsymbol{K_{t}} (y_{t} - f_{t}) \\\ \boldsymbol{C_{t}} &= (\boldsymbol{I} - \boldsymbol{K_{t}} \boldsymbol{F_{t}}) \boldsymbol{R_{t}} \end{align*} $$
$\boldsymbol{K_{t}}$はカルマンゲインと呼ばれるものです。$\boldsymbol{I}$は単位行列です。
平滑化
$t+1$での状態の平滑化分布の平均と共分散行列$\boldsymbol{s_{t+1}}, \boldsymbol{S_{t+1}}$(それぞれp次元ベクトル、p x pの行列)が与えられると、平滑化分布 $N(\boldsymbol{s_{t}}, \boldsymbol{S_{t}})$は以下で計算できます。
$$ \begin{align*} \boldsymbol{A_{t}} &= \boldsymbol{C_{t}} \boldsymbol{G_{t+1}}^{\boldsymbol{T}} \boldsymbol{R_{t+1}}^{-1} \\\ \boldsymbol{s_{t}} &= \boldsymbol{m_{t}} + \boldsymbol{A_{t}} (\boldsymbol{s_{t+1}} - \boldsymbol{a_{t+1}}) \\\ \boldsymbol{S_{t}} &= \boldsymbol{C_{t}} + \boldsymbol{A_{t}} (\boldsymbol{S_{t+1}} - \boldsymbol{R_{t+1}}) \boldsymbol{A_{t}}^{\boldsymbol{T}} \end{align*} $$
$\boldsymbol{A_{t}}$は平滑化利得と呼ばれるものです。
対数尤度
観測誤差と状態誤差をパラメータとして与えると、一期先予測尤度から尤度を解析的に計算できます。対数尤度は以下で求められます。
$$ \begin{align*} loglik(\boldsymbol{G_{t}}, \boldsymbol{F_{t}}, \boldsymbol{W_{t}}, V_{t}, \boldsymbol{m_{0}}, \boldsymbol{C_{0}}) &= \sum_{t=1}^{T} \log p(y_{t} | y_{1:t-1}; \boldsymbol{G_{t}}, \boldsymbol{F_{t}}, \boldsymbol{W_{t}}, V_{t}, \boldsymbol{m_{0}}, \boldsymbol{C_{0}}) \\\ &= -\frac{1}{2} T \log 2 \pi - \frac{1}{2} \sum_{t=1}^{T} log |Q_{t}| - \frac{1}{2} \sum_{t=1}^{T} (y_{t} - f_{t})^2 / Q_{t} \end{align*} $$
対数尤度を最大化するような観測誤差と状態誤差の値を数理最適化で求めるプロセスを最初に行い、この観測誤差と状態誤差をパラメータとして用いてフィルタリングと平滑化を行います。
以上のアルゴリズムの導出はこちらの書籍をご参照ください。
- 基礎からわかる時系列分析
―Rで実践するカルマンフィルタ・MCMC・粒子フィルター
- 日本語で読める状態空間モデルの本では最高レベルに充実していると思います。
- Rのコードでの実装例もあるので大変参考になります。
カルマンフィルタの実装
いま推定したいベータ値のモデルは、上の行列形式の状態空間モデルでそれぞれ以下としたものです。
- $y_{t}$: $r_{t}$
- $\boldsymbol{F_{t}}$: $(1, r_{t}^{M})$
- $\boldsymbol{x_{t}}$: $(\alpha_{t}, {\beta_{t}})^{\mathrm{T}}$
- $\boldsymbol{G_{t}}$: 2 x 2の単位行列
- $\boldsymbol{w_{t}}$: 左上が$W_{\alpha}$, 右下が$W_{\beta}$の2 x 2の対角行列
以下のコードがカルマンフィルタの実装です。上で示したアルゴリズムをそのまま実装します。
def filtering(y, m, C, G, F, W, V):
"""
(t-1)期において、1期先(t期)のフィルタリングを行う関数
such as:
x_t = G_t * x_(t-1) + w_t, w_t ~ N(0, W_t) : 状態方程式
y_t = F_t * x_t + v_t, v_t ~ N(0, V_t) : 観測方程式
x, G, w, W, Fは行列, y, v, Vはスカラー
Params:
y: 観測値 [時点t]
m, C: 状態の平均, 共分散行列 [t-1]
G, F, W, V: 状態遷移行列, 観測行列, 状態誤差の共分散行列, 観測誤差の共分散行列 [t]
Returns:
tuple
フィルタリング分布の平均と共分散行列 m, C [t]
一期先予測分布の平均と共分散行列 a, R [t]
一期先予測尤度の平均と共分散行列 f, Q [t]
"""
# 一期先予測分布
a = G @ m
R = G @ C @ G.T + W
# 一期先予測尤度
f = F @ a
Q = F @ R @ F.T + V
# カルマンゲイン
K = R @ F.T @ np.linalg.inv(Q)
# 状態の更新
m = a + K @ (y - f)
C = R - K @ F @ R
f_scalar, Q_scalar = f.item(), Q.item()
return m, C, a, R, f_scalar, Q_scalar
def smoothing(s, S, m, C, a, R, G):
"""
(t+1)期のsとSからt期のsとSを求める(状態の平滑化分布の平均と共分散行列)
Params:
s, S: 平滑化分布の平均, 共分散行列 [t+1]
m, C: 状態の平均, 共分散行列 [t]
a, R: 一期先予測分布の平均と共分散行列 [t+1]
G: 状態遷移行列 [t+1]
Returns:
tuple
平滑化分布の平均, 共分散行列 s, S [t]
"""
# 平滑化利得
A = C @ G.T @ np.linalg.inv(R)
# 平滑化された状態
s = m + A @ (s - a)
S = C + A @ (S - R) @ A.T
return s, S
def reverse_loglik(w_v, dims, y, G, F, m0, C0):
"""
状態誤差と観測誤差を与えると対数尤度の-1倍を返す関数
Params:
w_v: 長さ2のtuple 状態誤差と観測誤差の値
dims: 状態の数
y, G, F, m0, C0: 状態空間モデルの係数
Returns:
float: 対数尤度の-1倍
"""
# 分散は負にならないのでexpをかける
W = np.eye(dims) * np.exp(w_v[0])
V = np.array([1]).reshape((1, 1)) * np.exp(w_v[1])
T = len(y)
m, C = np.zeros((T, dims)), np.zeros((T, dims, dims))
a, R = np.zeros((T, dims)), np.zeros((T, dims, dims))
f, Q = np.zeros((T)), np.zeros((T))
# 全期間フィルタリングする
for t in range(0, T):
_F = F[t].reshape((1, dims))
if t == 0:
m[t], C[t], a[t], R[t], f[t], Q[t] = filtering(y[t], m0, C0, G, _F, W, V)
else:
m[t], C[t], a[t], R[t], f[t], Q[t] = filtering(y[t], m[t-1], C[t-1], G, _F, W, V)
loglik = (-1) * np.sum(np.log(Q)) / 2 - (np.sum((y - f)**2 / Q)) / 2
return (-1)*loglik
# 対数尤度を最大化する観測誤差と状態誤差を求める
ret_market = df.get_column("ret_market").to_numpy()
ret_stock = df.get_column("ret_stock").to_numpy()
y = ret_stock
x = ret_market
T = len(y)
dims = 2
G = np.eye(dims)
F = np.eye(T, dims)
F[:, 0] = 1
F[:, 1] = x
# 状態の平均と共分散行列の初期値
m0 = np.zeros(dims)
C0 = np.eye(dims)*10000000
best_par=sp.optimize.minimize(
reverse_loglik,
[0.0, 0.0],
args=(dims, y, G, F, m0, C0),
method="BFGS"
)
W = np.eye(dims) * np.exp(best_par.x[0])
V = np.array([1]).reshape((1, 1)) * np.exp(best_par.x[1])
# 上で求めた観測誤差と状態誤差をもとにフィルタリングと平滑化を行う
# 結果を入れる変数
m, C = np.zeros((T, dims)), np.zeros((T, dims, dims))
a, R = np.zeros((T, dims)), np.zeros((T, dims, dims))
f, Q = np.zeros((T)), np.zeros((T))
s, S = np.zeros((T, dims)), np.zeros((T, dims, dims))
# フィルタリング
for t in range(0, T):
_F = F[t].reshape((1, dims))
if t == 0:
m[t], C[t], a[t], R[t], f[t], Q[t] = filtering(y[t], m0, C0, G, _F, W, V)
else:
m[t], C[t], a[t], R[t], f[t], Q[t] = filtering(y[t], m[t-1], C[t-1], G, _F, W, V)
# 平滑化
for t in range(T - 1, 0, -1):
if t == T - 1:
s[t], S[t] = m[t], C[t]
else:
s[t], S[t] = smoothing(s[t+1], S[t+1], m[t], C[t], a[t+1], R[t+1], G)
20秒くらいで推定できます。
scipyのscipy.optimize.minimizeは最小化なので、対数尤度の-1倍を最小化の目的関数とします。scipy.optimize.minimizeに渡す初期値ですが、与える初期値によっては局所解に落ちるので、初期値を複数与えて目的関数が最小となる初期値をグリッドサーチで求めるのが望ましいです。
RやPythonなどのよくできたライブラリだとよくあるタイプのモデルは行列形式で書かなくても記述できますが、少しカスタマイズしようとすると、ライブラリを使っても行列表現して自分で係数行列を与えてあげることが必要になります。
スクラッチで実装するにしてもライブラリを使うにしても、カルマンフィルタの実装のポイントは、推定したいモデルを行列形式で書くこと、各パラメータの行列の次元(m x n)と何が行列で何がスカラーなのかを意識することだと思います。意識しないと混乱するんですよね。
ベータ値(カルマンフィルタ版)
フィルタ化と平滑化の状態の平均と共分散行列を取り出して95%信頼区間を計算します。扱いやすいようにnumpy.ndarrayからpolars.DataFrameに変換して持っておきます。
Code
# フィルタ化と平滑化の平均と共分散行列を取り出し、そこから95%信頼区間を計算する
beta_est = (
pl.DataFrame({
"date": df.get_column("date"),
"estimated": m[:, 1],
"std_error": np.sqrt(C[:, 1, 1])
})
.with_columns(
lower=pl.col("estimated")+sp.stats.norm.ppf(0.025)*pl.col("std_error"),
upper=pl.col("estimated")+sp.stats.norm.ppf(0.975)*pl.col("std_error"),
)
)
alpha_est = (
pl.DataFrame({
"date": df.get_column("date"),
"estimated": m[:, 0],
"std_error": np.sqrt(C[:, 0, 0])
})
.with_columns(
lower=pl.col("estimated")+sp.stats.norm.ppf(0.025)*pl.col("std_error"),
upper=pl.col("estimated")+sp.stats.norm.ppf(0.975)*pl.col("std_error"),
)
)
beta_smooth = (
pl.DataFrame({
"date": df.get_column("date"),
"estimated": s[:, 1],
"std_error": np.sqrt(S[:, 1, 1])
})
.with_columns(
lower=pl.col("estimated")+sp.stats.norm.ppf(0.025)*pl.col("std_error"),
upper=pl.col("estimated")+sp.stats.norm.ppf(0.975)*pl.col("std_error"),
)
)
alpha_smooth = (
pl.DataFrame({
"date": df.get_column("date"),
"estimated": s[:, 0],
"std_error": np.sqrt(S[:, 0, 0])
})
.with_columns(
lower=pl.col("estimated")+sp.stats.norm.ppf(0.025)*pl.col("std_error"),
upper=pl.col("estimated")+sp.stats.norm.ppf(0.975)*pl.col("std_error"),
)
)
次のプロットの1枚目はベータ値($\beta_{t}$)のフィルタ化推定量、2枚目は平滑化推定量、3枚目は東京電力の終値です。赤い線は平均値、上下の青いリボンは95%信頼区間です。ただし最初の50営業日は推定が安定していないので51営業日以降をプロットしています。
Code
# 結果のプロット
# 最初の50期は使わない
p1 = (
ggplot(beta_est.slice(50), aes("date"))+
theme_light()+
geom_ribbon(aes(ymin="lower", ymax="upper"), fill="lightsteelblue", alpha=0.5)+
geom_line(aes(y="lower"), color="lightsteelblue")+
geom_line(aes(y="upper"), color="lightsteelblue")+
geom_line(aes(y="estimated"), color="firebrick")+
scale_x_date(breaks="1 year", date_labels="%y")+
scale_y_continuous(breaks=range(-1, 3, 1))+
labs(
title="[9501: Tepco HD] time-varing beta (filtered); red: estimated (mean), light blue: 95%CI",
x="date (year)",
y="beta"
)
)
p2 = (
ggplot(beta_smooth.slice(50), aes("date"))+
theme_light()+
geom_ribbon(aes(ymin="lower", ymax="upper"), fill="lightsteelblue", alpha=0.5)+
geom_line(aes(y="lower"), color="lightsteelblue")+
geom_line(aes(y="upper"), color="lightsteelblue")+
geom_line(aes(y="estimated"), color="firebrick")+
scale_x_date(breaks="1 year", date_labels="%y")+
scale_y_continuous(breaks=range(-1, 3, 1))+
labs(
title="[9501: Tepco HD] time-varing beta (smoothed); red: estimated (mean), light blue: 95%CI",
x="date (year)",
y="beta"
)
)
p3 = (
ggplot(df.slice(50), aes("date", "close_stock"))+
theme_light()+
geom_line()+
scale_x_date(breaks="1 year", date_labels="%y")+
labs(
title="[9501: Tepco HD] stock price (close)",
x="date (year)",
y="close"
)
)
pw.load_ggplot(p1, figsize=(10, 2)) / pw.load_ggplot(p2, figsize=(10, 2)) / pw.load_ggplot(p3, figsize=(10, 2))
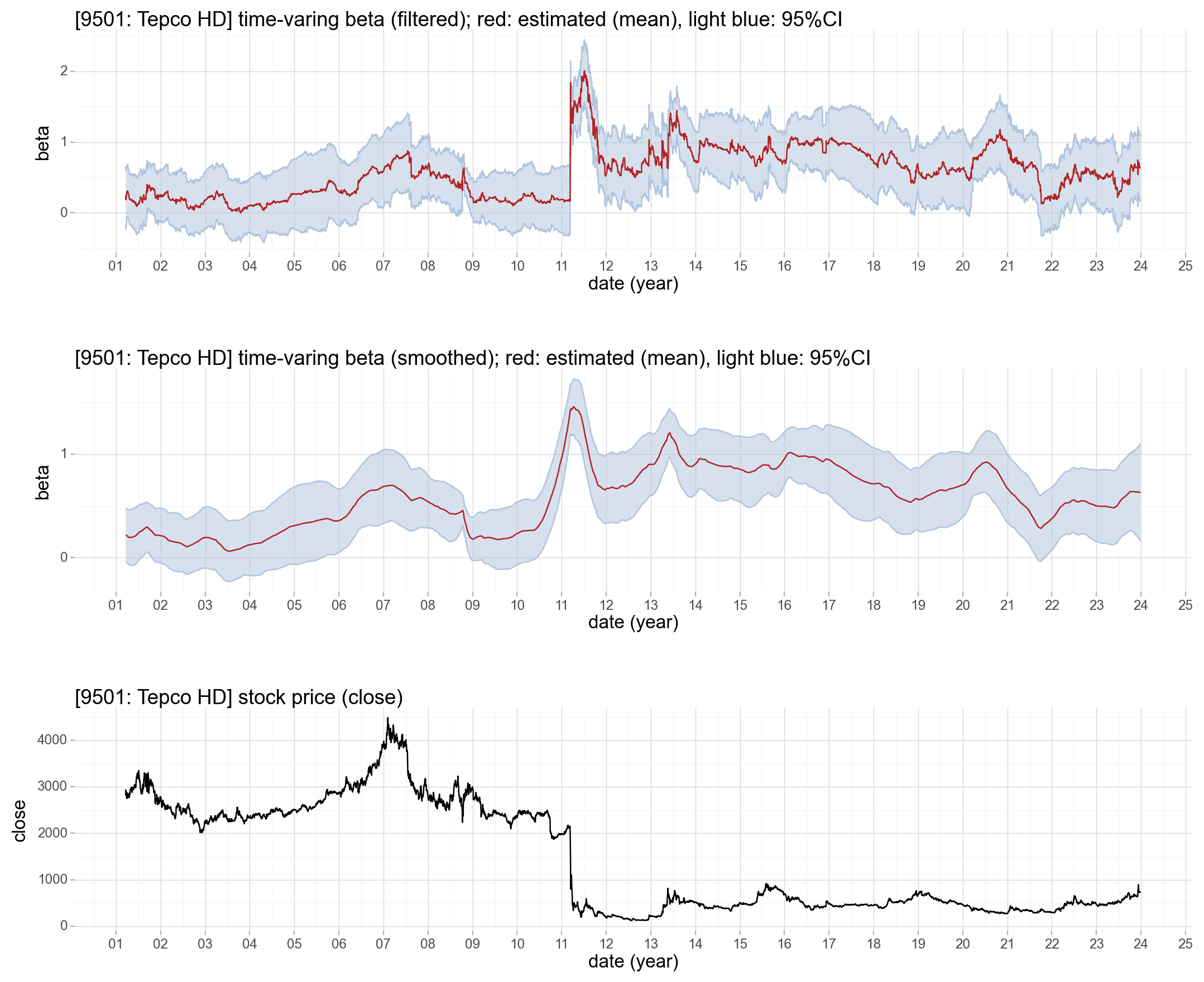
状態空間モデルを用いたことで、ベータ値の推定値だけでなく、ベータ値の95%信頼区間を求めることができます。ベータ値は95%の確率でこの範囲内という幅を得られるのもうれしいですね。
一番上のプロットを見ると分かりますが、2011年3月の東日本大震災までは、ベータ値の平均は1を下回っています。東京電力株は景気変動の影響を受けにくいディフェンシブ銘柄の代表ともいえる銘柄でしたが、東日本大震災のころにベータ値が急変動し、一時は2程度まで上がっていることが分かります。
2枚目のプロットは平滑化推定量なので、1枚目のプロットを滑らかにしたような感じになっていて大まかなトレンドが分かりやすいですね。ただし、全期間の観測値から状態を推定するという平滑化のアルゴリズム上、ベータ値は東日本大震災の前から大きく上昇しています。
東日本大震災のころにベータ値が急変動している背景は、原発事故やそれによる経営環境の変化だと想像はできますが、状態空間モデルではそうであるという因果関係は何も示していないことに注意が必要です。しかし、冒頭で触れた「経済・ファイナンスのためのカルマンフィルター入門」では、原発を持たない沖縄電力以外の電力会社は東京電力と同様に震災を境にベータの振る舞いが変わっていて、沖縄電力だけは特に変化がなかったと述べられています。
おわりに
状態空間モデルとカルマンフィルタによってベータ値の変動をとらえることができました。
状態誤差と観測誤差は正規分布としましたが、ベータ値の状態空間モデルでは特に状態誤差は正規分布ではないという先行研究4もあるので、状態誤差をt分布などにしたモデルを組んでみても面白そうです。
[Appendix. 1] R + KFASでのカルマンフィルタの実装
Rで実装する場合の例です。Rでカルマンフィルタをやるなら、KFASという、dlmに並んでデファクトスタンダードのライブラリがあります。
Pythonの場合と同じように、dfというdata.frameに、ret_stockとret_marketというカラムを持っている前提です。
library(KFAS)
# 状態空間モデルの定義
mod <- KFAS::SSModel(
# 観測誤差の分散
H=NA,
# SSMregression内の-1は状態方程式に切片がないことを示す
# Qは状態誤差の分散
ret_stock ~ KFAS::SSMregression(~ret_market-1, Q=NA),
data=df
)
# 対数尤度を最大化する観測誤差と状態誤差を数理最適化で求める
fit <- KFAS::fitSSM(mod, inits=c(0,0), method="BFGS")
# フィルタリングと平滑化をする
kfs <- KFAS::KFS(fit$model, filtering=c("state", "mean"), smoothing=c("state", "mean"))
これだけです。楽ですね。今回の回帰タイプの線形・ガウスの状態空間モデルはKFAS::SSMregression()という関数でサポートされていますのでこれを呼ぶだけです。
フィルタ化推定量の平均と共分散行列、平滑化推定量の平均と共分散行列をそれぞれkfs$att, kfs$Ptt, kfs$alphahat, kfs$Vで取り出して、Python版と同じようなベータ値の時系列プロットを描くことができます。
[Appendix. 2] ベータ値の定式化(リスクフリーレートバージョン)
ベータ値の推定モデルは、リスクフリーレート5を取り入れたバージョンもあります。
いま、$t$日におけるリスクフリーレートを$r_{t}^{f}$としたとき、最初の簡略化したモデルは以下になります。
$$ r_{t} - r_{t}^{f} = \beta_{t} (r_{t}^{M} - r_{t}^{f}) + \epsilon_t, \quad \epsilon_{t} \sim N(0, \sigma^2) $$
また、状態空間モデルバージョンはこちらになります。
$$ \begin{aligned} r_{t} - r_{t}^{f} &= \beta_{t} (r_{t}^{M} - r_{t}^{f}) + e_{t}, \quad e_t \sim N(0, \sigma_{e}^2) \\\ \beta_{t} &= \beta_{t-1} + \eta_{t}, \quad \eta_t \sim N(0, \sigma_{\eta}^2) \end{aligned} $$
どちらも、$\alpha_{t}$の項がなくなっています。
$r_{t} - r_{t}^{f}$と$r_{t}^{M} - r_{t}^{f}$はそれぞれ、リスクを負って得られる個別株式とマーケット指数の超過リターンです。そのため、$\alpha_{t}$が正であれば、リスクを全く負わずに、リターンがリスクフリーレート+$\alpha_{t}$だけ得られることを示します。そのような裁定取引の機会は効率的な市場では得られないというファイナンスの無裁定理論より、$\alpha_{t}$は0となります6。なお、これは理論だけの話ではなく、$\alpha_{t}$をモデルに入れて推定すると、多くの場合で$\alpha_{t}$は有意に正でも負でもないことが実証的にも示されます。
ただし、日本のリスクフリーレートはほぼ0のため、リスクフリーレートを考慮してもしなくても大きくは変わりません。
関連記事
このヘッジによって市場平均のリターンとの差分だけを得ることができます。例えば市場平均が-5%、個別株式のポジションが-3%となった場合、-3%-(-5%)=2%のリターンを得られます。個別株式のポジションが値下がった場合でも市場平均とのリターンの差分だけを得られるというのがメリットです。詳しく知りたい方はこちらの本の第3章をご参照ください: ジョン・ハル (2016), 「ファイナンシャルエンジニアリング(第9版)」。ただし実際には、個別株式や株価指数(先物)の最低投資単位の都合上ベータ値を厳密に0にするポジションは組みづらいこと、ヘッジ比率を調整することの手数料の考慮、連続的な値動きに対してヘッジ比率の調整は日次や週次、月次など離散的なタイミングでしか行えず厳密にヘッジができないことなどの難しさがあります。 ↩︎
リターンと聞いてふつうイメージするのは、$r_{t} = (S_{t} / S_{t-1}) - 1$だと思います。金融工学では当日の株価の自然対数と前日の株価の自然対数の差である対数リターンを用います。株価がたいてい取りうる数%くらいのリターンの範囲では、テイラー展開より対数リターンは割り算でのリターンとほぼ一致します。 ↩︎
なお、「経済・ファイナンスのためのカルマンフィルター入門」(森平, 2019)では、$\alpha$は時変ではないモデルを推定しています。 ↩︎
矢野浩一 (2004), 「カルマンフィルタによるベータ推定」2004年度FSAリサーチレビュー, 104-125. ↩︎
ここでいうリスクフリーレートには、現在では無担保コール翌日物金利やOISレートが用いられます。リスクフリーレートとみなされることの多い国債の利回りは、日本国の信用リスクが含まれるため厳密にはリスクフリーなレートではありません。無担保コール翌日物金利やOISは信用リスクをほとんど含まない金利のため、リスクフリーレートとして望ましいです。リスクフリーレートにどの金利を使うかというのはリーマンショック以降特に意識されるようになったと聞きます。リスクフリーレートについて知りたい方はこの辺が参考になるかと思います。リスク・フリー・レート(RFR)入門-TONA,TORF,OISを中心に-/金利スワップ入門 -基礎編- ↩︎
逆に言うと、競争が働いている効率的な市場ではない市場では、そうではない可能性はあります。 ↩︎